




Next: Example
Up: Sava: CA residual migration
Previous: Introduction
Common-azimuth data represent subsets of 3-D datasets that have been
recorded or transformed to zero cross-line offsets (hy=0).
Stolt constant velocity migration for common-azimuth data involves
the use of the following dispersion relation Biondi and Palacharla (1995):
| 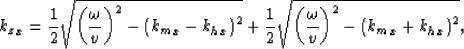 |
(1) |
where the depth wavenumber of the common-azimuth dataset (kz) is
| 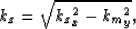 |
(2) |
and the midpoint and offset wavenumbers are defined as 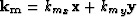 and
and 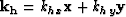 .
.
We can write equations (2) and (1)
for a given reference velocity (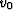 ) as
) as
| 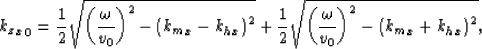 |
(3) |
and
| 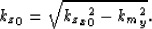 |
(4) |
The goal of common-azimuth Stolt residual migrations is to obtain kz
(equations 2 and 1) from
kz0 (equations 4 and 3).
If we express the frequency 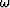 from equation (3) as
from equation (3) as
![\begin{displaymath}
\omega^2 = \v_0^2 \frac
{\left[{k_z}_0^2+{k_m}_y^2+{k_h}_x^2...
...ft[{k_z}_0^2+{k_m}_y^2+{k_m}_x^2 \right]}
{{k_z}_0^2+{k_m}_y^2}\end{displaymath}](img9.gif)
and introduce it in equation (1), we obtain
the common-azimuth residual migration equations
| 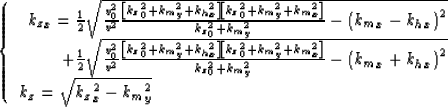 |
(5) |
Note that for 2-D prestack data,
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) equations (5) reduce to the 2-D prestack
form Sava (1999):
equations (5) reduce to the 2-D prestack
form Sava (1999):
![\begin{displaymath}
\begin{array}
{r}
k_z= \frac{1}{2}\sqrt{\frac{\v_0^2}{\v^2...
...ht]}
{{k_z}_0^2}- \left({k_m}_x+{k_h}_x\right)^2}
\end{array},\end{displaymath}](img14.gif)
which, furthermore, reduces to the well-known Stolt 2-D post-stack
residual migration equation Stolt (1996)
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
![\begin{displaymath}
k_z= \sqrt{\frac{\v_0^2}{\v^2}
{ \left[{k_z}_0^2+{k_m}_x^2 \right]}- {k_m}_x^2}.\end{displaymath}](img17.gif)
As for the 2-D prestack data, the common-azimuth residual migration is
velocity independent; that is, we need not make any assumption about the
actual values of the velocities for the reference and improved migration,
but only about their ratio. In this way, we can take an image and residually
migrate it without knowing what velocity model has been used to image it
in the first place.





Next: Example
Up: Sava: CA residual migration
Previous: Introduction
Stanford Exploration Project
10/25/1999
![]() ) as
) as
![]() from equation (3) as
from equation (3) as
![\begin{displaymath}
\omega^2 = \v_0^2 \frac
{\left[{k_z}_0^2+{k_m}_y^2+{k_h}_x^2...
...ft[{k_z}_0^2+{k_m}_y^2+{k_m}_x^2 \right]}
{{k_z}_0^2+{k_m}_y^2}\end{displaymath}](img9.gif)
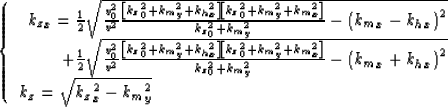
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) equations (5) reduce to the 2-D prestack
form Sava (1999):
equations (5) reduce to the 2-D prestack
form Sava (1999):
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
: