




Next: Results
Up: Brown & Clapp: Seismic
Previous: Introduction
Consider local windows of the seismic image to be the simple superposition of signal
and noise:
| 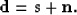 |
(1) |
The frequency domain representation of the Wiener optimal reconstruction filter for
uncorrelated signal and noise is Castleman (1996); Leon-Garcia (1994):
| 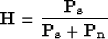 |
(2) |
where 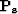 and
and 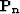 are the power spectra of the unknown signal and noise,
respectively. Multiplication of
are the power spectra of the unknown signal and noise,
respectively. Multiplication of 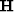 with the data spectrum gives an optimal
(in the least squares sense) estimate of the spectrum of the unknown signal.
with the data spectrum gives an optimal
(in the least squares sense) estimate of the spectrum of the unknown signal.
Abma (1995) and Claerbout (1998) solved a constrained least squares problem
to separate signal from spatially uncorrelated noise:
| 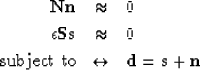 |
|
| (3) |
| |
where the operators 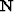 and
and 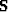 represent t-x domain convolution with
prediction-error filters (PEF's) which decorrelate the unknown noise
represent t-x domain convolution with
prediction-error filters (PEF's) which decorrelate the unknown noise 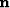 and signal
and signal  ,
respectively, and the factor
,
respectively, and the factor  balances the energies of the residuals.
Explicitly minimizing the quadratic objective function suggested by equation (3)
leads to the following expression for the predicted signal:
balances the energies of the residuals.
Explicitly minimizing the quadratic objective function suggested by equation (3)
leads to the following expression for the predicted signal:
| 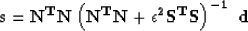 |
(4) |
Since the frequency response of the PEF approximates the inverse spectrum of the data used
to estimate it, we see that Abma's approach is similar to Wiener reconstruction.
If the noise is assumed a priori to be spatially uncorrelated, as in Abma (1995),
the noise decorrelator 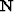 is simply the identity. Gaussian noise is in the nullspace of
the PEF estimation, so the signal decorrelator
is simply the identity. Gaussian noise is in the nullspace of
the PEF estimation, so the signal decorrelator 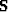 can be estimated reliably from the
data, i.e.,
can be estimated reliably from the
data, i.e., 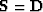 , where
, where 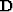 is a data decorrelating filter.
Otherwise, if the noise is correlated spatially, an explicit noise model is required to estimate
is a data decorrelating filter.
Otherwise, if the noise is correlated spatially, an explicit noise model is required to estimate
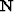 , and an approach like the one used by Spitz (1999) to estimate
, and an approach like the one used by Spitz (1999) to estimate 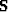 .
Modifying equation (3) to reflect Spitz's choice of
.
Modifying equation (3) to reflect Spitz's choice of 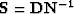 and applying
the constraint
and applying
the constraint 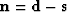 gives
gives
| 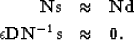 |
|
| (5) |
When solved iteratively, the problem can be preconditioned to improve convergence.
Following Fomel et al. (1997), we can make the change of variables
| 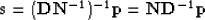 |
(6) |
and rewrite equation (5):
| 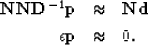 |
|
| (7) |
Brown et al. (1999) solved equation (7) iteratively to
suppress ground roll with complicated moveout patterns, where 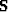 and
and 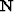 are
nonstationary t-x-domain PEF's. Clapp and Brown (1999) did the same for
multiple reflections.
are
nonstationary t-x-domain PEF's. Clapp and Brown (1999) did the same for
multiple reflections.
Unfortunately, the estimation of nonstationary PEF's is computationally costly, and it
is often difficult to ensure that the filters are minimum-phase, a necessary requirement
for stable deconvolution, as in equation (7).
For the application at hand, the final result is not the estimated signal and noise,
but simply the noise-to-signal ratio.
It follows that the separation need not be perfect - just good enough to distinguish
between regions of the data with gross similarity to the facies template from the rest
of the data.
A properly stacked or migrated seismic image should have no ``crossing dips,''
and so can be conceptualized as a single-valued spatial function of local dip angle.
Not surprisingly, we have found that simple three-point ``steering filters''
Clapp et al. (1997), work well for the noise and data decorrelating filters,
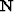 and
and 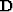 , required to solve equation (7).
The only thing needed to set up the steering filters is an estimate of the local dip field
of the data and facies template, for which the automatic dip scanning technique of
Claerbout (1992) produces satisfactory results.
, required to solve equation (7).
The only thing needed to set up the steering filters is an estimate of the local dip field
of the data and facies template, for which the automatic dip scanning technique of
Claerbout (1992) produces satisfactory results.
Assuming that a given 2-D wavefield u(t, x) is planar with unknown local dip p,
the operator
| 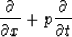 |
(8) |
will extinguish it. If 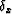 and
and 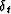 are finite difference
stencils for the continuous partial derivatives above, then equation (8)
can be rewritten as a convolution, and hence cast as a univariate optimization
for p:
are finite difference
stencils for the continuous partial derivatives above, then equation (8)
can be rewritten as a convolution, and hence cast as a univariate optimization
for p:
| 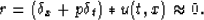 |
(9) |
Differentiating the quadratic functional rT r with respect to
p gives an optimal estimate of the local dip:
| 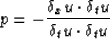 |
(10) |





Next: Results
Up: Brown & Clapp: Seismic
Previous: Introduction
Stanford Exploration Project
10/25/1999
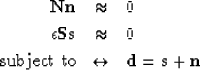
![]() is simply the identity. Gaussian noise is in the nullspace of
the PEF estimation, so the signal decorrelator
is simply the identity. Gaussian noise is in the nullspace of
the PEF estimation, so the signal decorrelator ![]() can be estimated reliably from the
data, i.e.,
can be estimated reliably from the
data, i.e., ![]() , where
, where ![]() is a data decorrelating filter.
Otherwise, if the noise is correlated spatially, an explicit noise model is required to estimate
is a data decorrelating filter.
Otherwise, if the noise is correlated spatially, an explicit noise model is required to estimate
![]() , and an approach like the one used by Spitz (1999) to estimate
, and an approach like the one used by Spitz (1999) to estimate ![]() .
Modifying equation (3) to reflect Spitz's choice of
.
Modifying equation (3) to reflect Spitz's choice of ![]() and applying
the constraint
and applying
the constraint ![]() gives
gives
![]() and
and ![]() , required to solve equation (7).
The only thing needed to set up the steering filters is an estimate of the local dip field
of the data and facies template, for which the automatic dip scanning technique of
Claerbout (1992) produces satisfactory results.
, required to solve equation (7).
The only thing needed to set up the steering filters is an estimate of the local dip field
of the data and facies template, for which the automatic dip scanning technique of
Claerbout (1992) produces satisfactory results.