




Next: About this document ...
Up: Brown et al.: Signal/Noise
Previous: REFERENCES
The frequency domain representation of the Wiener optimal reconstruction filter for
uncorrelated signal and noise is Castleman (1996); Leon-Garcia (1994)
| 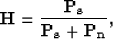 |
(8) |
where 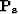 and
and 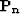 are the power spectra of the unknown signal and noise,
respectively. Multiplication of
are the power spectra of the unknown signal and noise,
respectively. Multiplication of 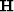 with the data spectrum extracts the signal
spectrum which is optimal in the least squares sense.
with the data spectrum extracts the signal
spectrum which is optimal in the least squares sense.
Abma 1995 solved a constrained least squares problem
to separate signal from spatially uncorrelated noise.
| 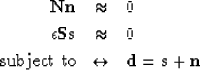 |
|
| (9) |
| |
which reduces to equation (2). Explicitly minimizing the quadratic
objective function suggested by equations (9) or (2)
leads to the following expression for the predicted signal:
| ![\begin{displaymath}
\bf s = \left[\frac{ N'N}{ N'N + \epsilon^2 S'S}\right] \ d
\end{displaymath}](img25.gif) |
(10) |
Recalling that the frequency response of the PEF is a smoothed approximation to the
inverse spectrum of the data from which it was estimated
| 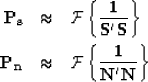 |
(11) |
| |
it is easy to show that the Wiener reconstruction result is equivalent to Abma's.
Claerbout 1998a uses this approach, and we extended a variation of it to obtain
the results obtained in this paper. When spatially coherent events cross, as they do
with ground roll and primaries, they are not uncorrelated. We believe that in order to
maintain a high degree of rigor in our future formulation of this problem, the correlation
between signal and noise should be accounted for. A more general form of the Wiener optimal
reconstructor Castleman (1996); Leon-Garcia (1994) is
| 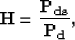 |
(12) |
where 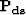 is the Fourier transform of the cross-correlation of the data
and the unknown signal. Such a formulation is considerably less intuitive than
equation (8), and we currently have no concrete ideas as to a starting
point.
is the Fourier transform of the cross-correlation of the data
and the unknown signal. Such a formulation is considerably less intuitive than
equation (8), and we currently have no concrete ideas as to a starting
point.
Nemeth 1996 presents a more rigorous formulation for the separation of
coherent noise and signal. As it is collected, the data is composed of overlapping
signal and noise events, so the goal is to map the data to a domain where the signal
and noise are uncorrelated, and thus separable without crosstalk.
Nemeth's model is a composite vector, ![$[{\bf m_s \;\; m_n}]^T$](img29.gif) , consisting of the
independent signal and noise model in the transformed (migrated) domain.
His composite modeling operator,
, consisting of the
independent signal and noise model in the transformed (migrated) domain.
His composite modeling operator, ![$[{\bf L_s \;\; L_n}]$](img30.gif) , is adjoint to migration,
so his method accounts for the arbitrary moveout of real data - not the idealized
hyperbolic moveout assumed for Radon-family transforms. The least squares inverse for
Nemeth's model is
, is adjoint to migration,
so his method accounts for the arbitrary moveout of real data - not the idealized
hyperbolic moveout assumed for Radon-family transforms. The least squares inverse for
Nemeth's model is
| ![\begin{displaymath}
\left[\begin{array}
{c}
\bold m_s \\ \bold m_n
\end{array...
...y}
{c}
\bold L^T_s \\ \bold L^T_n
\end{array}\right] \bf d
\end{displaymath}](img31.gif) |
(13) |
In the context of prediction-error filtering, the ``model'' would be the residual of
some PEF convolved with the data, such that the signal and noise are separated in the
model space. The cross terms in Nemeth's ``inverse model covariance matrix,''
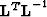 , account for correlation between signal and noise.
In practice, Nemeth's method is weakened by the need for an explicit ground roll
model. However, if Nemeth's migration operators are cleverly replaced with prediction
error filters, a similarly powerful formulation could probably be derived, one which
is free from the need to model ground roll explicitly.
, account for correlation between signal and noise.
In practice, Nemeth's method is weakened by the need for an explicit ground roll
model. However, if Nemeth's migration operators are cleverly replaced with prediction
error filters, a similarly powerful formulation could probably be derived, one which
is free from the need to model ground roll explicitly.
In any case, Spitz' 1999 choice of signal predictor,
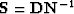 gives good results, and probably handles the correlation between signal
and noise correctly.
Though we don't show the result in this paper, we have found that when the
actual noise model is used (synthetic data), the estimated signal is nearly perfect.
gives good results, and probably handles the correlation between signal
and noise correctly.
Though we don't show the result in this paper, we have found that when the
actual noise model is used (synthetic data), the estimated signal is nearly perfect.





Next: About this document ...
Up: Brown et al.: Signal/Noise
Previous: REFERENCES
Stanford Exploration Project
10/25/1999
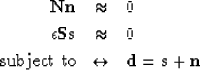
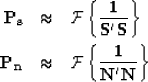
![]() , consisting of the
independent signal and noise model in the transformed (migrated) domain.
His composite modeling operator,
, consisting of the
independent signal and noise model in the transformed (migrated) domain.
His composite modeling operator, ![]() , is adjoint to migration,
so his method accounts for the arbitrary moveout of real data - not the idealized
hyperbolic moveout assumed for Radon-family transforms. The least squares inverse for
Nemeth's model is
, is adjoint to migration,
so his method accounts for the arbitrary moveout of real data - not the idealized
hyperbolic moveout assumed for Radon-family transforms. The least squares inverse for
Nemeth's model is
![\begin{displaymath}
\left[\begin{array}
{c}
\bold m_s \\ \bold m_n
\end{array...
...y}
{c}
\bold L^T_s \\ \bold L^T_n
\end{array}\right] \bf d
\end{displaymath}](img31.gif)
![]() gives good results, and probably handles the correlation between signal
and noise correctly.
Though we don't show the result in this paper, we have found that when the
actual noise model is used (synthetic data), the estimated signal is nearly perfect.
gives good results, and probably handles the correlation between signal
and noise correctly.
Though we don't show the result in this paper, we have found that when the
actual noise model is used (synthetic data), the estimated signal is nearly perfect.