




Next: Synthetic example
Up: Clapp & Brown: Multiple
Previous: INTRODUCTION
Signal to noise separation has a long history at SEP Claerbout (1991); Harlan (1986); Kostov (1990).
The method we use is similar to Abma's 1995 formation.
Abma (1995)
proposed solving the set of equations:
| 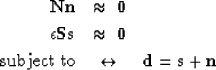 |
|
| (1) |
| |
where the operators 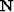 and
and 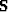 represent t-x domain convolution with
(PEF's) which decorrelate the unknown noise
represent t-x domain convolution with
(PEF's) which decorrelate the unknown noise 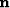 and signal
and signal  , respectively, and the factor
, respectively, and the factor  balances the energies of the residuals.
balances the energies of the residuals.
For his problem he assumed that the noise was uncorrelated, therefore 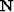 becomes the identity and
becomes the identity and 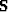 is the PEF that best predicted the
data in a given window [patching approach Claerbout (1992); Schwab and Claerbout (1995)].
is the PEF that best predicted the
data in a given window [patching approach Claerbout (1992); Schwab and Claerbout (1995)].
In the multiple problem the noise is not uncorrelated so we must find
another way to find 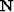 . Spitz (1999) proposed defining
. Spitz (1999) proposed defining
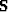 as
as 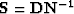 where
where 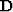 is a filter that
characterizes the data rather than the signal. Using this new definition
we get a new set of fitting goals:
is a filter that
characterizes the data rather than the signal. Using this new definition
we get a new set of fitting goals:
| 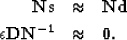 |
|
| (2) |
Following Fomel et al. (1997) we can set
up the conversion by reformulating it as a preconditioned problem
by a simple change of variables (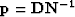 )
)
| 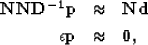 |
|
| (3) |
where 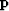 is just a dummy preconditioning variable.
is just a dummy preconditioning variable.
Instead of using patching we followed the methodology of
Crawley et al. (1998) and constructed and estimated
a space varying filter.
| 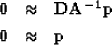 |
|
| (4) |
where 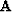 is a radial smoother Clapp et al. (1999).
For
is a radial smoother Clapp et al. (1999).
For 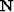 we follow a similar procedure assuming an a priori model for the
noise.
we follow a similar procedure assuming an a priori model for the
noise.





Next: Synthetic example
Up: Clapp & Brown: Multiple
Previous: INTRODUCTION
Stanford Exploration Project
10/25/1999
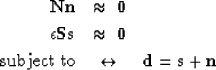
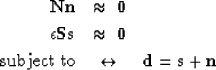
![]() becomes the identity and
becomes the identity and ![]() is the PEF that best predicted the
data in a given window [patching approach Claerbout (1992); Schwab and Claerbout (1995)].
is the PEF that best predicted the
data in a given window [patching approach Claerbout (1992); Schwab and Claerbout (1995)].
![]() . Spitz (1999) proposed defining
. Spitz (1999) proposed defining
![]() as
as ![]() where
where ![]() is a filter that
characterizes the data rather than the signal. Using this new definition
we get a new set of fitting goals:
is a filter that
characterizes the data rather than the signal. Using this new definition
we get a new set of fitting goals: