 |
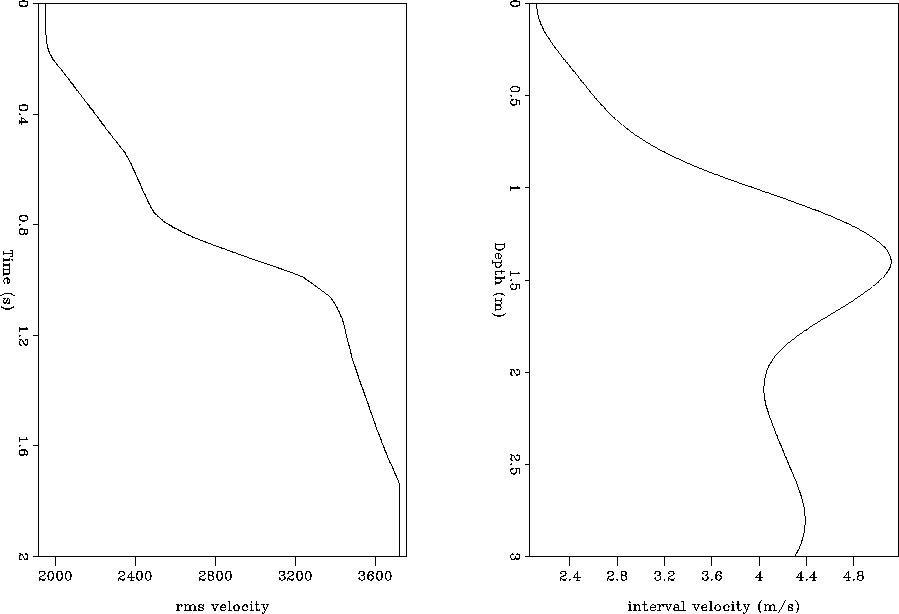
Figure 15 One-dimensional RMS and interval velocity functions of the survey
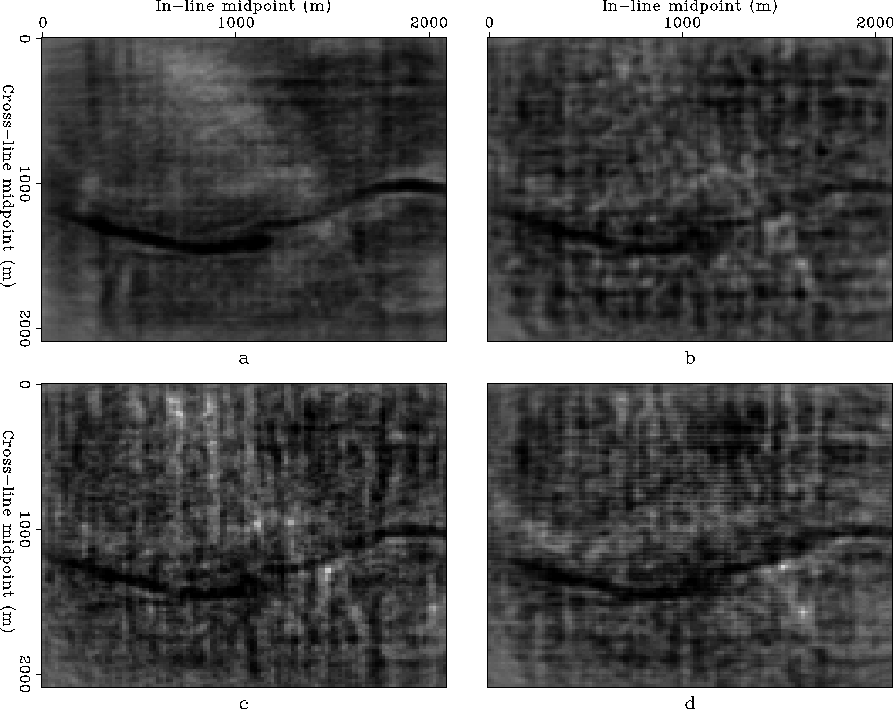
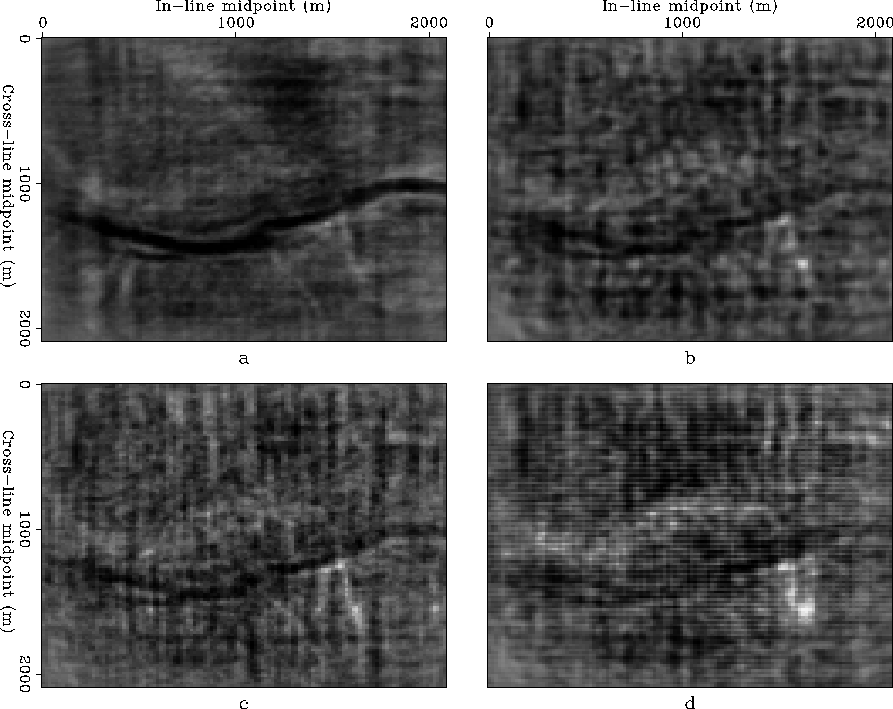
I have presented a new technique for processing irregularly sampled wide-azimuth surveys that accurately images 3-D seismic data and preserves its relative amplitudes. The method applies AMO to regularize the data as common-azimuth (CA) and common-offset (CO) cubes. It addresses both issues of algorithmic accuracy and proper handling of irregular geometry and therefore allows for reliable amplitude analysis on migrated data.
AMO is applied as an integral operator in the time-space domain. It is implementation as discrete summation on irregularly sampled data is improved by diagonal scaling. The diagonal transformation reduces the effects of irregular coverage at the surface and varying illumination at depth. The partial stack is normalized by a reference model that is the AMO response to an input vector with all components equal to one (flat event). The advantage of including AMO in the processing flow is threefold: (1) reduction of the size of prestack data subsets (2) interpolation to a regular grid before imaging (3) common-azimuth common-offset processing of the 3D survey.
The next chapter poses partial stacking by AMO as an optimization process to regularize the geometry of 3D surveys in presence of spatial aliasing. The limited small aperture of AMO enables inexpensive implementation of the inversion algorithm. Beyond the fold normalization, the diagonal transformation is used as a preconditioner to accelerate the convergence of the iterative solution.
 |
 |
 |