True-amplitude imaging

The derivation of the forward-modeling operator provides insight into the form of the inversion operator. In generating the seismic model, each trace is modeled as a weighted sum of image sources on a reflector. Therefore, Kirchhoff imaging of seismic data involves a weighted sum of filtered surface-recorded traces where the weights are deduced from inversion theory. The resulting algorithms are then applied to the discrete seismic data through the linear transformation

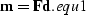$$\bold m = \bold F \bold d. \EQNLABEL{equ1}$$ (40)

True amplitude imaging aims at deriving the proper weights along the summation surfaces or impulse responses of 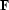${\bf F}$. In the previous chapter, I presented detailed derivations for true-amplitude weights for the azimuth moveout operator. Using a similar approach, Jaramillo and Bleistein 1997 derived amplitude-preserving weights for migration and demigration based on the Kirchhoff modeling formula. Then using the superposition principle they derived two alternative operators to perform migration as isochron superposition and demigration as diffraction superposition. I find the two approaches rather easier to understand using Claerbout's terminology for push and pull operators defined below.