




Next: Integral inverse DMO
Up: Amplitude-preserving AMO
Previous: Overview
The derivation of AMO as the cascade of DMO and 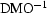 results into the following expression for the amplitude term,
results into the following expression for the amplitude term,
| 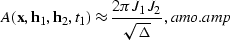 |
(13) |
where  is the output location
vector in
midpoint coordinates, J1 and J2 are the Jacobians in the FK
definition of DMO and
is the output location
vector in
midpoint coordinates, J1 and J2 are the Jacobians in the FK
definition of DMO and 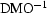 and
and 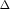 is the determinant of a
Hessian matrix that is independent of the particular DMO of choice.
For given input half-offset and time (
is the determinant of a
Hessian matrix that is independent of the particular DMO of choice.
For given input half-offset and time (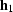 , t1) and
output half-offset
, t1) and
output half-offset 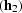 ,equation amo.amp describes the weights along the impulse response
of AMO in the time-space domain.
The Jacobians J1 and J2 and the determinant
,equation amo.amp describes the weights along the impulse response
of AMO in the time-space domain.
The Jacobians J1 and J2 and the determinant 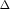 in
equation amo.amp are
evaluated at the stationary point of the phase function in the integral
kernel of AMO.
in
equation amo.amp are
evaluated at the stationary point of the phase function in the integral
kernel of AMO.
The amplitude behavior of AMO is thoroughly controlled by the Jacobian
terms of DMO and its inverse.
Liner and Cohen 1988 argued that the adjoint
is a poor representation for an inverse DMO.
They showed that the application
of Hale's DMO followed by its adjoint inverse results in serious amplitude
degradation and therefore
they proposed an asymptotic ``true-inverse'' for Hale's DMO.
Similar to their formulation, I
derive asymptotic inverses for Zhang's and Bleistein's DMO operators
which, as demonstrated later in the text, do preserve the amplitudes better.





Next: Integral inverse DMO
Up: Amplitude-preserving AMO
Previous: Overview
Stanford Exploration Project
1/18/2001
![]() results into the following expression for the amplitude term,
results into the following expression for the amplitude term,