




Next: INTERPOLATING MISSING TRACES
Up: Crawley : Nonstationary filters
Previous: INTRODUCTION
The time dip of seismic data changes rapidly along many axes, so a single PEF can only represent a small amount of data.
Often we divide the data into patches, where it is assumed the data have constant dips.
Because seismic data have curvature and may not be well represented by piecewise-constant dips, it is appealing to extend the idea of time-variable filtering to include spatial dimensions as well, and have smoothly varying PEFs to represent curved events.
I decrease the patch size, to as small as a single data sample,
changing the problem from overdetermined to very underdetermined.
It is possible to estimate all these filter coefficients
by the usual formulation,
supplemented with some damping equations, say
| 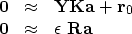 |
(1) |
where 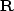 is a roughening operator,
is a roughening operator, 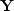 is convolution with the data, and
is convolution with the data, and 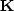 is a known filter coefficient mask.
is a known filter coefficient mask.
When the roughening operator 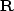 is a differential operator,
the number of iterations can be large.
To speed the calculation immensely and make the equations somewhat neater, we can ``precondition'' the problem.
Define a new variable
is a differential operator,
the number of iterations can be large.
To speed the calculation immensely and make the equations somewhat neater, we can ``precondition'' the problem.
Define a new variable 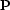 by
by
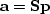 and insert it into (1) to get
and insert it into (1) to get
| 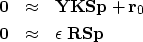 |
(2) |
| (3) |
Now, because the smoothing and roughening operators
are somewhat arbitrary, we may as well replace
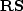 by
by 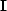 and get
and get
| 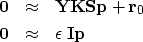 |
(4) |
| (5) |
We solve for 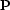 using conjugate gradients.
To see
using conjugate gradients.
To see  , just use
, just use 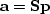 .To simplify things, one could just
drop the damping (5)
and keep only (4);
then to control the null space,
start from a zero solution and limit the number of iterations.
.To simplify things, one could just
drop the damping (5)
and keep only (4);
then to control the null space,
start from a zero solution and limit the number of iterations.
For 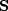 we can use polynomial division by a Laplacian or by filters with a preferred direction.
If the data are CMP gathers, it is attractive to use radial filters, which are explained later.
we can use polynomial division by a Laplacian or by filters with a preferred direction.
If the data are CMP gathers, it is attractive to use radial filters, which are explained later.





Next: INTERPOLATING MISSING TRACES
Up: Crawley : Nonstationary filters
Previous: INTRODUCTION
Stanford Exploration Project
4/20/1999
![]() is a differential operator,
the number of iterations can be large.
To speed the calculation immensely and make the equations somewhat neater, we can ``precondition'' the problem.
Define a new variable
is a differential operator,
the number of iterations can be large.
To speed the calculation immensely and make the equations somewhat neater, we can ``precondition'' the problem.
Define a new variable ![]() by
by
![]() and insert it into (1) to get
and insert it into (1) to get
![]() we can use polynomial division by a Laplacian or by filters with a preferred direction.
If the data are CMP gathers, it is attractive to use radial filters, which are explained later.
we can use polynomial division by a Laplacian or by filters with a preferred direction.
If the data are CMP gathers, it is attractive to use radial filters, which are explained later.