




Next: Discussion
Up: Applications
Previous: 2-D Stacked Seismic Section
To fill ``holes'' in collected data, we have the familiar SEP formulation
Claerbout (1998a):
| ![\begin{eqnarray}
\bf Km - d &\approx& 0
\\ [0.05in]
\bf \epsilon Am &\approx& 0
\end{eqnarray}](img9.gif) |
(5) |
| (6) |
[5] is the ``data matching'' goal, which states that the model  must match the known data
must match the known data 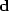 , while [6] is the ``model smoothness''
goal, where
, while [6] is the ``model smoothness''
goal, where 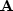 is an arbitrary roughening operator. To combat slow convergence,
Claerbout 1998a preconditions with the inverse of the convolutional
operator
is an arbitrary roughening operator. To combat slow convergence,
Claerbout 1998a preconditions with the inverse of the convolutional
operator 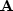 (multidimensional deconvolution). Provided that
(multidimensional deconvolution). Provided that
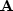 is minimum phase or factorizable into the product of minimum phase filters
Sava et al. (1998),
the helix transform now permits stable multidimensional deconvolution. Making
the change of variables
is minimum phase or factorizable into the product of minimum phase filters
Sava et al. (1998),
the helix transform now permits stable multidimensional deconvolution. Making
the change of variables 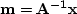 , we have the equivalent preconditioned problem:
, we have the equivalent preconditioned problem:
| ![\begin{eqnarray}
\bf KA^{-1}x - d &\approx& 0
\\ [0.05in]
\bf \epsilon x &\approx& 0
\end{eqnarray}](img14.gif) |
(7) |
| (8) |
The operator 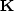 effectively maps vectors in model space into
a smaller-dimension ``known data space'', so it has a nonempty nullspace.
Missing points in model space are completely unconstrained by
effectively maps vectors in model space into
a smaller-dimension ``known data space'', so it has a nonempty nullspace.
Missing points in model space are completely unconstrained by 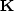 , so
our choice of
, so
our choice of 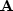 wholly determines the behavior of the missing model points, i.e.,
their texture Fomel et al. (1997).
The PEF is a perfect choice for
wholly determines the behavior of the missing model points, i.e.,
their texture Fomel et al. (1997).
The PEF is a perfect choice for 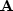 , as shown in Figure
10. The preconditioned, PEF-regularized result fills the
hole quite believably after only 20 iterations, as opposed to the case where
, as shown in Figure
10. The preconditioned, PEF-regularized result fills the
hole quite believably after only 20 iterations, as opposed to the case where
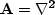 , which imposes an unrealistically smooth texture on the missing
model points.
, which imposes an unrealistically smooth texture on the missing
model points.
tree-hole-filled
Figure 10 Clockwise from top left:
Data with hole, impulse response of ``inverse PEF'' (deconvolution of the PEF
estimated from the data and a spike), data in-filled using 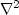 regularization, data in-filled using preconditioned PEF regularization.
regularization, data in-filled using preconditioned PEF regularization.










Next: Discussion
Up: Applications
Previous: 2-D Stacked Seismic Section
Stanford Exploration Project
4/20/1999
