Fourier transform method

The texture synthesis methodology of this paper really boils down to one of spectral estimation. An image's amplitude spectrum contains the relative weights between frequency components, while the phase spectrum localizes these frequency components in space Castleman (1996). Therefore, it stands to reason that the texture of stationary, loosely correlated images is adequately modeled using the amplitude spectrum alone. This idea is the basis for the Fourier Transform method of texture synthesis: all ``realizations'' of texture synthesis are forced to have the same amplitude spectrum, differing only in phase. The following is an outline of the method.

1.

Given a training image, t(x,y), compute its amplitude spectrum:

 

R(k_x,k_y) = T^*(k_x,k_y) T(k_x,k_y) (1)

2.

Create random phase function: $\phi_r(k_x,k_y) \;=\; random \; numbers$.

3.

Reconstruct by substituting random phase:  

$$t_{\tiny \mbox{recon}}(x,y) = {\cal F}^{-1} \left\{ \; \sq... ... R(k_x,k_y)\right\vert} \; e^{i \phi_r(k_x,k_y) } \; \right\}$$ (2)

Figures 2 and 3 illustrate the Fourier transform method of texture synthesis. Clockwise from top-left: the training image, the synthesized image, the TI's amplitude spectrum, and the TI's phase spectrum.

 

rand2d-ftsyn Figure 2 Smoothed random image and Fourier transform synthesis. The TI is stationary, so the synthesis result is convincing. Notice that the true phase, in the regions where the modulating amplitude spectrum is nonzero, is quite random in appearence.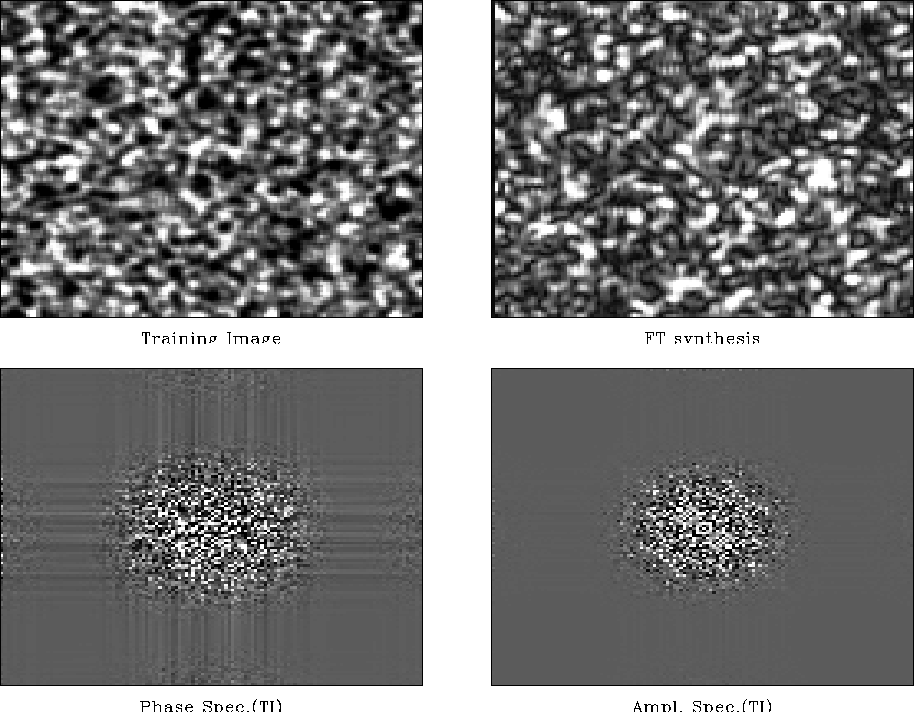

 

ridges-ftsyn Figure 3 "Ridges" image and Fourier transform synthesis. The correlation is both long-range and extremely complicated - quite like a meandering network of fluvial channels. Though the synthesized image has the same general character as the TI, not all of the structures are modeled, proving the inadequacy of the amplitude spectrum for modeling nonstationary, highly correlated images. The TI phase spectrum shows some ordering, so the random phase substitution was ill-advised.