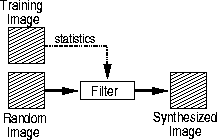
In terms of digital images, the word texture might be defined as, ``an attribute representing the spatial arrangement of gray levels of the pixels in a region,'' IEEE (1990). In the same context, I define texture synthesis as the process of first estimating the spatial statistical properties of a known image and then imparting these statistics onto a second (random) image. Figure 1 illustrates the general approach taken here: an uncorrelated image is transformed into one with the same statistical qualities as a known ``training image'' (TI), through an as-yet undefined filtering operation.
|
syn-templ
Figure 1 The generalized texture synthesis algorithm. From the training image (TI), statistics are extracted and encoded into a filtering operation, which forces an uncorrelated image to have the same statistical qualities, or texture, as the TI. |  |
Texture synthesis is an active area of research in the computer graphics community, owing to the need for realistic, quickly generated surface textures Mao and Brown (1998); Heeger and Bergen (1995); Simoncelli and Portilla (1998), but the same notion of texture applies to the earth sciences as well. Physically measurable quantities, be they geology, gravity, or topography, behave in certain repeatable ways as a function of space, i.e., these quantities have a given texture. Inversion problems are often underdetermined, hampered by a lack of ``hard'' measurements, causing a nullspace of high dimension. A priori ``soft'' constraints on functional form of the unknown model help in suppressing the nullspace of modeling operators. These a priori constraints can be conceptualized as textures. For instance, in velocity analysis and tomography, the earth's velocity field is sometimes assumed to have a ``blocky'' texture Clapp et al. (1998). Underdetermined inverse interpolation problems are often regularized by assuming ``smooth'' model texture Claerbout (1998a).
The prediction-error filter (PEF) is an autoregressive filter which has the distinction of capturing the inverse spectrum of the data it is regressed upon. Because it captures this essential statistical property of the data, the PEF is a candidate for the generic "filter" operation shown in Figure 1.
This paper is intended as a follow-up to the earlier work by Claerbout and Brown 1999, which presented a texture synthesis technique utilizing 2-D PEF's and 2-D deconvolution via the helix transform Claerbout (1998b). First I motivate the texture synthesis problem by applying a Fourier transform-based technique to create synthetic textures of everyday objects, then introduce and apply a PEF-based technique to synthesize the same images. I compare the results of the two methods and conclude that the PEF-based method is the better choice because it more naturally handles missing data. Next I apply the PEF-based method to a 2-D stacked seismic section. The nature of the residual error in the PEF estimation of this example suggests application to seismic discontinuity detection and migration velocity analysis. Last, I solve a simple missing data problem to illustrate how regularization with a PEF imparts a reasonable ``texture'' onto the nullspace.