




Next: FILLING VOLUMES
Up: Claerbout: Helical meshes on
Previous: Helical coordinate on a
I could not find the equations for a helix on a cone,
so I derive them below.
An example of results is Figure 2.
trycart
Figure 2
Helix on a cone.
Top shows the embedded helix.
Bottom hides it.
Apex angle 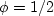 .
.





Define 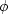 to be the angle from
the axis of the cone to its surface.
I call this the apex angle.
I discovered by accident that certain apex angles
give interesting patterns in the crossline directions
while most do not.
I found these
patterns to be insensitive to the choice of N
and show them here for about N=1400.
Another value of apex angle
with an interesting pattern is
to be the angle from
the axis of the cone to its surface.
I call this the apex angle.
I discovered by accident that certain apex angles
give interesting patterns in the crossline directions
while most do not.
I found these
patterns to be insensitive to the choice of N
and show them here for about N=1400.
Another value of apex angle
with an interesting pattern is 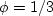 .It gives the charming pattern in Figure 3.
(I've seen this pattern before on a party hat.
I attributed it to an ingenious artist.
Now I realize that like all mathematics,
this art existed before the big bang.)
.It gives the charming pattern in Figure 3.
(I've seen this pattern before on a party hat.
I attributed it to an ingenious artist.
Now I realize that like all mathematics,
this art existed before the big bang.)
YinYang
Figure 3
Helix on a cone.
Top shows the embedded helix.
Bottom hides it.
Apex angle equals one third radian.





The radius r of the cone divided by its altitude z
has a ratio
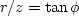 where
where 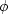 is the angle from
the axis of the cone to its surface.
The area of a circle is
is the angle from
the axis of the cone to its surface.
The area of a circle is
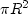 .The surface area of a cone is
.The surface area of a cone is
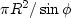 .Dividing the area into N cells,
the surface area per cell is
.Dividing the area into N cells,
the surface area per cell is
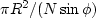 .Taking any cell area to be square,
the length of a side is
.Taking any cell area to be square,
the length of a side is
| 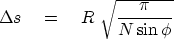 |
(3) |
The number of points running one cycle around a rim is
| 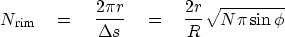 |
(4) |
On one cycle around the rim,
the radius must change by 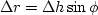 where
the hypotenuse
where
the hypotenuse 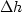 of the triangle
lies on the surface of the cone.
Thus, for each mesh point going around the rim
of the triangle
lies on the surface of the cone.
Thus, for each mesh point going around the rim
| 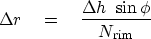 |
(5) |
Since we want ``square'' mesh points, 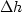 must equal
must equal 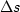 , hence
, hence
| 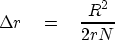 |
(6) |
The algorithm starts on the rim at 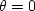 and r=R.
At each step, update r and
and r=R.
At each step, update r and 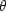 with
with
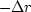 and
and 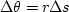 .Stop before
.Stop before 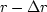 becomes negative.
becomes negative.





Next: FILLING VOLUMES
Up: Claerbout: Helical meshes on
Previous: Helical coordinate on a
Stanford Exploration Project
4/20/1999
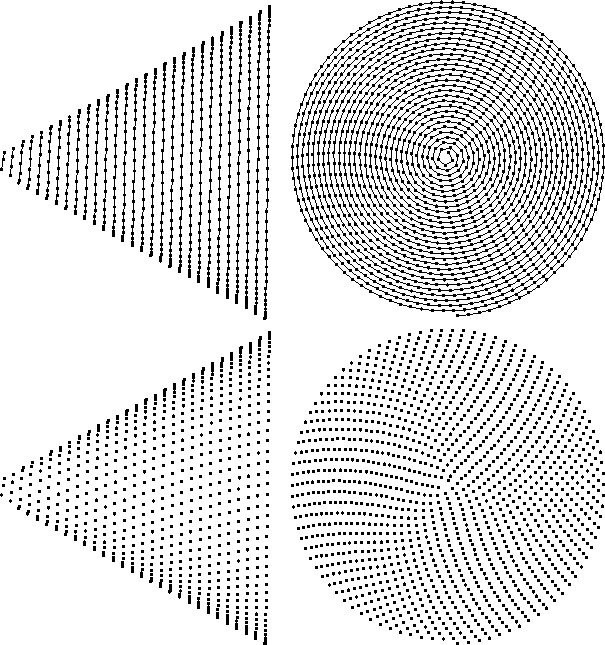
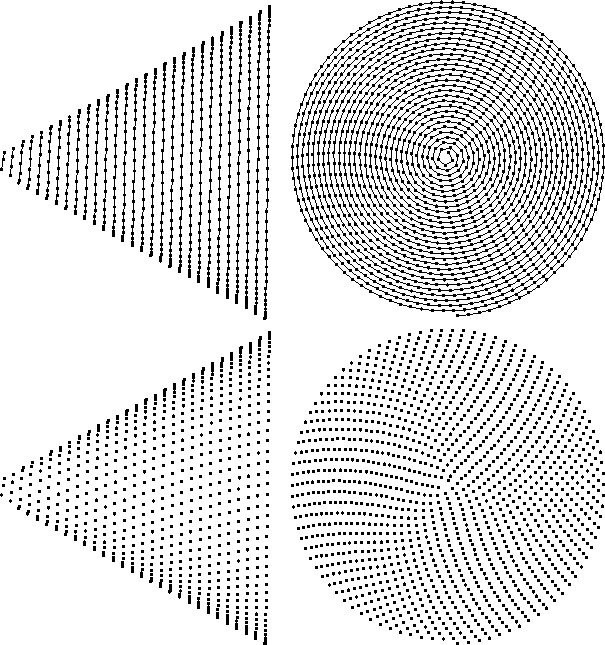
![]() to be the angle from
the axis of the cone to its surface.
I call this the apex angle.
I discovered by accident that certain apex angles
give interesting patterns in the crossline directions
while most do not.
I found these
patterns to be insensitive to the choice of N
and show them here for about N=1400.
Another value of apex angle
with an interesting pattern is
to be the angle from
the axis of the cone to its surface.
I call this the apex angle.
I discovered by accident that certain apex angles
give interesting patterns in the crossline directions
while most do not.
I found these
patterns to be insensitive to the choice of N
and show them here for about N=1400.
Another value of apex angle
with an interesting pattern is ![]() .It gives the charming pattern in Figure 3.
(I've seen this pattern before on a party hat.
I attributed it to an ingenious artist.
Now I realize that like all mathematics,
this art existed before the big bang.)
.It gives the charming pattern in Figure 3.
(I've seen this pattern before on a party hat.
I attributed it to an ingenious artist.
Now I realize that like all mathematics,
this art existed before the big bang.)

![]() where
where ![]() is the angle from
the axis of the cone to its surface.
The area of a circle is
is the angle from
the axis of the cone to its surface.
The area of a circle is
![]() .The surface area of a cone is
.The surface area of a cone is
![]() .Dividing the area into N cells,
the surface area per cell is
.Dividing the area into N cells,
the surface area per cell is
![]() .Taking any cell area to be square,
the length of a side is
.Taking any cell area to be square,
the length of a side is