Johnson et al. (1987) have shown that, for a single-porosity medium, the frequency dependence of the dynamic permeability and tortuosity can be well-approximated by
k() = k_0 [1 - 4ik_0^2_^2_f/^2^2]^12 - ik_0__f/ and
() = _ + ik_0_f
[1 - 4ik_0^2_^2_f/^2^2]^12.
The symbol ![]() stands for the fluid viscosity (in units of
stands for the fluid viscosity (in units of
![]() ), while
), while ![]() is the kinematic viscosity
(in units of m2/s).
The new symbols appearing in these formulas are the
d.c. permeability k0, the high frequency tortuosity
is the kinematic viscosity
(in units of m2/s).
The new symbols appearing in these formulas are the
d.c. permeability k0, the high frequency tortuosity ![]() ,and the lambda parameter
,and the lambda parameter ![]() introduced by Johnson et al.
(1986). The values of the high frequency tortuosity
introduced by Johnson et al.
(1986). The values of the high frequency tortuosity ![]() for double-porosity media were considered here in Appendix A.
The d.c. permeabilities for double-porosity media have been
considered in Berryman and Wang (1995) and in Lewallen and Wang
(1998).
for double-porosity media were considered here in Appendix A.
The d.c. permeabilities for double-porosity media have been
considered in Berryman and Wang (1995) and in Lewallen and Wang
(1998).
For single porosity media, Johnson et al. (1987) show that the lambda parameter approximately satisfies
^2 = 8k_0F = 8k_0_/. For the present purposes, we will assume that this relation holds independently for the storage porosity and the fracture porosity. Then we have
^(1) = [8 k^(11) ^(1)/^(1)]^12 and
^(2) = [8 k^(22) ^(2)/^(2)]^12 = [8 k^(22)]^12.
Finally, we see that for the double-porosity medium, the corrections due to frequency dependence can be viewed alternatively as a frequency dependent viscosity, since equations (komega) and (tauomega) follow by assuming that
() (1-i^2_f/16)^12 These corrections need to be made separately for the two types of pores. This interpretation of the frequency dependence as being associated specifically with the viscosity is the one advocated by Biot (1956b), and has some advantages in the present context as it makes it quite straightforward to determine what the corrections should be for the multiple porosity problem. Note that we used (GLapproximation) to simplify the factors inside the square root in (etaGw).
It is not yet clear how to generalize these expressions for the permeability coupling terms k(12), but our assumption following (b23) that b23 = 0 has eliminated this potential problem from the present paper. Achieving an understanding of this issue will be one goal of our future work.
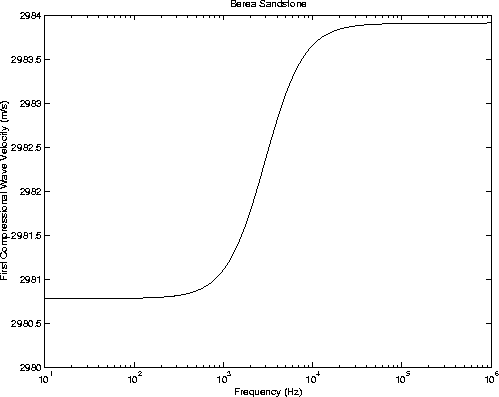
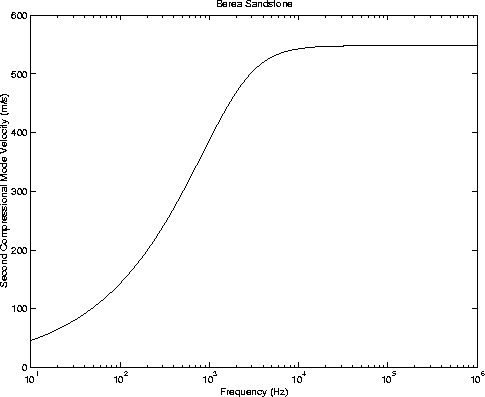
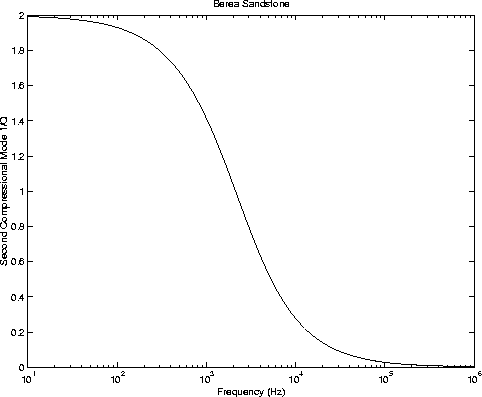
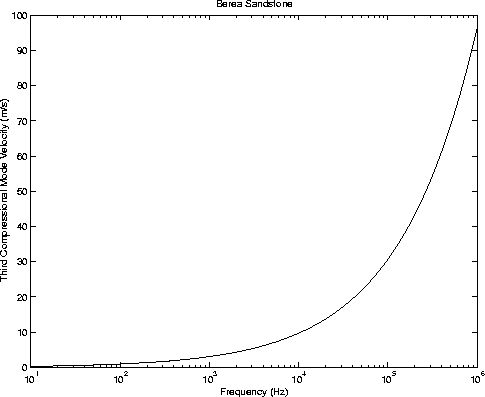
| Parameter | Formula | Berea |
| Berea Parameter |
 |
 |
 |
 |
 |
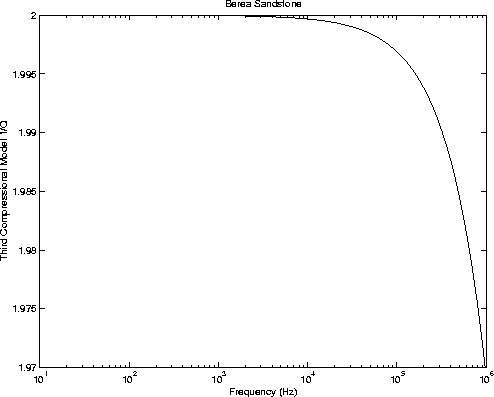 |