There is a large number of competing finite difference and related schemes for the solution of the eikonal equation suggested in the literature; we have chosen to use the essentially nonoscillatory (``ENO'') schemes of Osher and Sethian 1988 and Osher and Shu 1991 and the related weighed ENO (WENO) schemes Jiang and Peng (1997); Liu et al. (1994); Shu (1997) for the following reasons: (1)stable schemes of arbitrarily high order accuracy exist, permitting accurate solutions on coarse grids (which is critical to the mesh refinement or coarsenment); (2) versions exist in any dimension so that we can extend our methodology to the three-dimensional case straightforwardly El-Mageed et al. (1997); El-Mageed (1996); Qian and Symes (1998).
Our adaptive scheme is based on the 2nd and 3rd order WENO difference schemes introduced by Jiang and Peng 1997. These are in turn extensions of 2nd and 3rd order ENO difference schemes, which we present first.
For a function f of the space variable (x,z) in the computational domain, we write
The second and third order ENO refinements of ![]() are
are
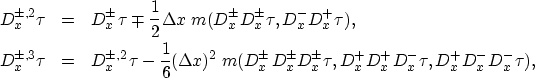 |
||
The upwind ENO approximations for ![]() are
are
The second order and third order ENO Runge-Kutta steps are
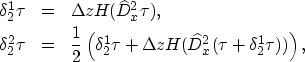 |
||
| (5) |
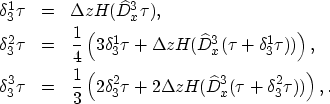 |
||
| (6) |
The depth step ![]() must satisfy the stability condition:
must satisfy the stability condition:
The nth order scheme is then
| (7) |
However, we have observed that the gradient of the take-off angle based on the third order ENO traveltime is too noisy to give us a smooth amplitude function. To alleviate this phenomenon, instead of ENO 3rd order refinements, we use WENO 5th order refinement Jiang and Peng (1997) to compute ![]() in the third order Runge-Kutta step, which gives us a smooth amplitude field.
in the third order Runge-Kutta step, which gives us a smooth amplitude field.
The WENO 5th order schemes for ![]() are
are
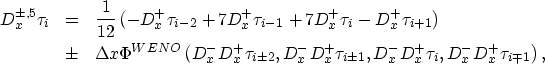 |
||
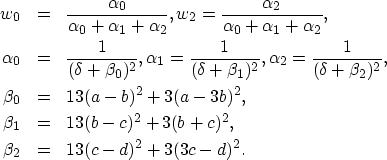 |
||