Denote by (xs,zs) the coordinates of a source point, and by (x,z) the coordinates of a general point in the subsurface. The first arrival traveltime field ![]() is the viscosity solution of the eikonal equation
is the viscosity solution of the eikonal equation
| (1) |
In some seismic applications, the traveltime field is only needed in regions where
To enforce this condition, we modify the eikonal equation as an evolutionary equation in depth, as suggested by Gray and May 1994:
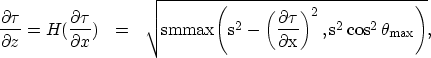 |
(2) |
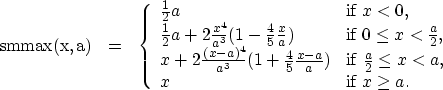 |
This equation defines a stable nonlinear evolution in z, suitable for explicit finite difference discretization. The solution ![]() is identical to the solution of the eikonal equation provided that the ray makes an angle
is identical to the solution of the eikonal equation provided that the ray makes an angle ![]() with the vertical.
with the vertical.