In the normal incidence case of Backus averaging, the layer properties of
thickness, ![]() , compliance,
, compliance, ![]() , and mass density,
, and mass density,
![]() , are replaced by the corresponding properties
of the equivalent homogeneous medium,
, are replaced by the corresponding properties
of the equivalent homogeneous medium, ![]() ,
, ![]() ,and
,and ![]() :
:
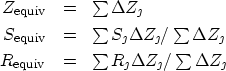 |
(1) | |
| (2) | ||
| (3) |
that is, the thickness of ![]() is the sum thickness
of the layers,
is the sum thickness
of the layers, ![]() , and the equivalent medium
mechanical
properties are the thickness-weighted averages of those of the layered medium.
, and the equivalent medium
mechanical
properties are the thickness-weighted averages of those of the layered medium.
However, these layers can also be described in terms of the layer
properties of one-way travel-time,
![]() , and impedance,
, and impedance, ![]() , with slowness,
, with slowness,
![]() acting as the means for changing the independent variable
between depth and time. It is well known that:
acting as the means for changing the independent variable
between depth and time. It is well known that:
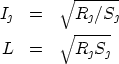 |
(4) | |
| (5) |
and from these:
| (6) | ||
| (7) |
and thus:
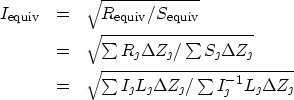 |
||
| (8) |
but ![]() , so:
, so:
| (9) |
and by similar reasoning the slowness equivalent:
| (10) |
and, since ![]() =
= ![]() :
:
| (11) |