




Next: HOW TO SMOOTH RADIALLY
Up: Clapp, et al.: Radial
Previous: WHY SMOOTH RADIALLY
Prediction-error filters work best on predicting local plane waves
Canales (1984); Claerbout (1992c). With non-stationary
filters, it is possible to predict data with variable slopes. For
preconditioning the filter estimation problem, such filters can be
smoothed along the direction where the slope stays locally constant.
To put this principle into a mathematical form, let us denote the
monodop data as P(x,y), where x and y are the coordinate
values. On a seismic data section, the y coordinate would have the
meaning of time, but here we would like to develop a general method
that would work on different kinds of data. The local dip field of the
data can be defined by the formula
| 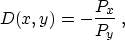 |
(4) |
where Px and Py denote the first partial derivatives: 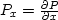 ,
, 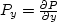 .To validate formula (4), consider a plane-wave model with
the slope s:
.To validate formula (4), consider a plane-wave model with
the slope s:
| 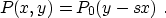 |
(5) |
Substituting (5) into formula (4), we can
see that the D(x,y) indeed produces an estimate of s
Claerbout (1992a). In the general case, D(x,y)
corresponds to the tangent of the local plane wave angle, measured
from the x axis in the direction of the y axis.
Bednar (1997) describes an application of formula
(4) for computing coherency attributes.
Instead of using formula (4) explicitly, we intend to
estimate prediction-error filters that would destroy local plane waves
in the data Claerbout (1992c); Schwab (1998). To
precondition the filter estimation problem we can smooth the filters
in the direction of the least change in the slope. By analogy with
(4), the smoothing direction can be defined as follows:
| 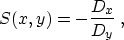 |
(6) |
or, substituting formula (4),
| 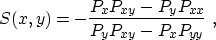 |
(7) |
where Pxx, Pyy, and Pxy are the corresponding
second-order partial derivatives. An important analytical test case is
a constant-velocity CMP gather, composed of reflection hyperbolas:
| 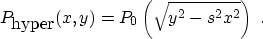 |
(8) |
Substituting (8) into formula (7) leads to
the expression
| 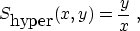 |
(9) |
which suggests smoothing the estimated prediction-error filters along
radial lines on the 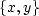 plane Crawley et al. (1998).
sigmod
plane Crawley et al. (1998).
sigmod
Figure 4 Synthetic model from Basic Earth
Imaging (left), its estimated dip field (center), and estimated
smoothing directions (right).




 wz
wz
Figure 5 Seismic shot gather (left), its estimated dip
field (center), and estimated smoothing directions (right).





Figure 4 and 5 illustrate a practical
application of formulas (4) and (6) on a
synthetic reflectivity model from Basic Earth Imaging
Claerbout (1995) and on a shot gather from the Yilmaz
collection Yilmaz (1987).
In both cases the first- and second-derivative
operators were computed with simple finite-difference schemes. To
avoid a non-stable division in formulas (4) and
(6), we solve the regularized least-square system
| 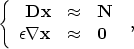 |
(10) |
where 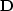 and
and 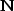 denote the denominator and the
numerator respectively,
denote the denominator and the
numerator respectively,  is the scalar regularization
parameter, and
is the scalar regularization
parameter, and  is the estimated regularized ratio. Our
simple two-point finite-difference scheme does not handle correctly
the aliased dips on the seismic gather in Figure 5.
Nevertheless it produces a reasonable output, which we can use as a
rough estimate of the smoothing directions.
is the estimated regularized ratio. Our
simple two-point finite-difference scheme does not handle correctly
the aliased dips on the seismic gather in Figure 5.
Nevertheless it produces a reasonable output, which we can use as a
rough estimate of the smoothing directions.





Next: HOW TO SMOOTH RADIALLY
Up: Clapp, et al.: Radial
Previous: WHY SMOOTH RADIALLY
Stanford Exploration Project
4/20/1999

