




Next: Preconditioning
Up: THEORY
Previous: THEORY
In general, the tomography problem is under-determined and requires
some type of regularization. Ideally, this regularization should
be the inverse model covariance Tarantola (1987) but that is not
readily available. In many cases we do have well logs, initial
migration surfaces, or a geologist's model of the region that can
at least indicate the trend that velocity should follow. Following
the method described in Clapp, et al. 1999 we
can build a space-varying operator composed of small plane wave annihilation
filters that can smooth our velocity along this predetermined trend.
The problem is that our model is not slowness, but change in slowness.
To a degree, we can get around this problem by following the method
similar to the one described by
Bevc 1994.
We start by stating our goal to smooth the slowness
field:
| 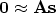 |
(4) |
where 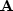 is our steering filter operator. But
is our steering filter operator. But  is actually
is actually
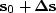 , so we can write a new regularization goal as
, so we can write a new regularization goal as
| 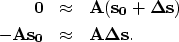 |
(5) |
| |
A problem with this method is
where the adjoint of our modeling operator (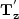 )
does not contribute at all to the model we
can introduce artifacts. Our best solution to date for
this problem is to introduce a smooth masking operator that tapers
off to zero in locations unaffected by
)
does not contribute at all to the model we
can introduce artifacts. Our best solution to date for
this problem is to introduce a smooth masking operator that tapers
off to zero in locations unaffected by 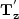 .
.





Next: Preconditioning
Up: THEORY
Previous: THEORY
Stanford Exploration Project
4/20/1999
![]() )
does not contribute at all to the model we
can introduce artifacts. Our best solution to date for
this problem is to introduce a smooth masking operator that tapers
off to zero in locations unaffected by
)
does not contribute at all to the model we
can introduce artifacts. Our best solution to date for
this problem is to introduce a smooth masking operator that tapers
off to zero in locations unaffected by ![]() .
.