The first step of migration consists of downward continuation of the wavefield measured at the surface (a.k.a. the data), which is done by the recursive application of the equation
| u0z+1 = T0z u0z | (1) |
| |
(2) |
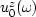 is the wavefield
is the wavefield 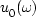 at depth z,
at depth z,
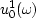 is the wavefield
is the wavefield 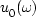 at the surface (z=0),
at the surface (z=0),
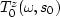 is the downward continuation operator at depth z,
is the downward continuation operator at depth z,
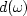 is the data, i.e., the wavefield at the surface, and
is the data, i.e., the wavefield at the surface, and
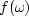 is a frequency-dependent scale factor for the data.
is a frequency-dependent scale factor for the data.
The second step of the migration by downward continuation is imaging.
According to the exploding reflector concept, the image is found by
selecting the wavefield at time t=0, or equivalently, by summing
over the frequencies ![]() :
:
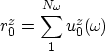 |
(3) |
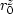 is the image (reflectivity) corresponding to a given
depth level z.
is the image (reflectivity) corresponding to a given
depth level z.