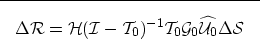Scattering and downward continuation
If we perturb the velocity model we introduce a perturbation in the
wavefield. In other words, the perturbation in slowness generates
a secondary wavefield, the scattered wavefield. We can downward
continue the scattered field as we did with the background wavefield
by writing
| 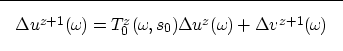 |
(20) |
where
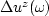 is the perturbation in the wavefield generated by the
perturbation in velocity, and
is the perturbation in the wavefield generated by the
perturbation in velocity, and
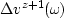 represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from the depth level z.
represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from the depth level z.
The scattered wavefield can be written as
| 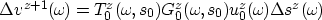 |
(21) |
where
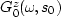 is the scattering operator at depth z, and
is the scattering operator at depth z, and
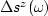 is the perturbation in slowness at depth z.
is the perturbation in slowness at depth z.
Huang et al. 1999 show that the scattering operator is
| 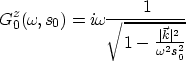 |
(22) |
and that it can be approximated by
| 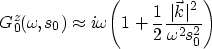 |
(23) |
which represents the first-order Born approximation. In this
equation, 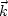 represents the horizontal component of the
wavenumber.
represents the horizontal component of the
wavenumber.
If we introduce Equation (B-2) into
(B-1) we obtain
| ![\begin{displaymath}
\Delta u^{z+1} = T_0^{z}
\left[ \Delta u^{z} + G_0^{z} u_0^{z} \Delta s^{z} \right] \end{displaymath}](img24.gif) |
(24) |
which, after rearrangements, becomes the recursion
| 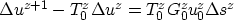 |
(25) |
We can express the recursive relationship between the perturbation in
velocity and the perturbation in the wavefield (B-6) as
| ![\begin{displaymath}
\fbox {$
[\bf {I}-\bf {T_0}]\Delta \bf{U}= \bf {T_0}\bf {G_0}\widehat {\bf{U_0}}\Delta \bf{\S}$}
\end{displaymath}](img62.gif) |
(26) |
where
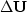 is a column vector containing the perturbation in the
wavefield at all depths,
is a column vector containing the perturbation in the
wavefield at all depths,
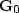 is a diagonal matrix containing the scattering term for
all the depth levels,
is a diagonal matrix containing the scattering term for
all the depth levels,
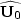 is a diagonal matrix containing the background wavefield
data for all the depth levels, and
is a diagonal matrix containing the background wavefield
data for all the depth levels, and
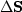 is a column vector containing the perturbation in the
velocity for all the depth levels.
is a column vector containing the perturbation in the
velocity for all the depth levels.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Note the different arrangement of the background wavefield data at all
depths (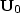 and
and 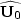 ).
).
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Similarly to the case of the background wavefield, the relationship
between the perturbation in the wavefield and the perturbation in
slowness can be written for all the frequencies in the data as
| 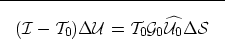 |
(27) |
where
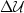 is a column vector containing the perturbation in the
wavefield for all the frequencies,
is a column vector containing the perturbation in the
wavefield for all the frequencies,
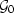 is a diagonal matrix containing the scattering operator
for all the frequencies,
is a diagonal matrix containing the scattering operator
for all the frequencies,
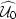 is a diagonal matrix containing the background wavefield
for all the frequencies, and
is a diagonal matrix containing the background wavefield
for all the frequencies, and
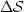 is a column vector containing the perturbation in slowness,
same for all the frequencies if we disregard dispersion.
is a column vector containing the perturbation in slowness,
same for all the frequencies if we disregard dispersion.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Again, it is important to note the different arrangement of the
background wavefield data at all frequencies (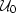 and
and 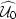 ).
).
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Therefore, we can compute the perturbation in the wavefield (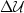 )
as a function of the perturbation in slowness (
)
as a function of the perturbation in slowness (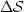 ) like this:
) like this:
| 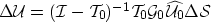 |
(28) |
Imaging
As for the background image, the perturbation in image (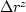 ),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies (
),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies ( ):
):
| 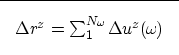 |
(29) |
We can write Equation (B-10) in matrix form as
| 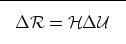 |
(30) |
where
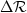 is a column vector containing the perturbation in image at
every depth level z.
is a column vector containing the perturbation in image at
every depth level z.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Therefore, the perturbation in image (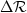 ), corresponding to the
perturbation velocity field (
), corresponding to the
perturbation velocity field (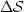 ), can be computed as follows:
), can be computed as follows:
| 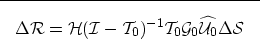 |
(31) |
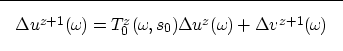
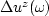 is the perturbation in the wavefield generated by the
perturbation in velocity, and
is the perturbation in the wavefield generated by the
perturbation in velocity, and
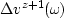 represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from the depth level z.
represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from the depth level z.
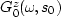 is the scattering operator at depth z, and
is the scattering operator at depth z, and
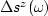 is the perturbation in slowness at depth z.
is the perturbation in slowness at depth z.
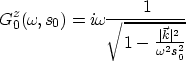
![\begin{displaymath}
\fbox {$
[\bf {I}-\bf {T_0}]\Delta \bf{U}= \bf {T_0}\bf {G_0}\widehat {\bf{U_0}}\Delta \bf{\S}$}
\end{displaymath}](img62.gif)
![\begin{eqnarray}
\left[ \matrix {
{1} & 0 & 0 &...& 0 & 0 \cr
{-T_0^{1}} & {1} &...
...2}\cr \Delta s^{3}\cr...\cr \Delta s^{N_z} \cr
} \right]\nonumber \end{eqnarray}](img63.gif)
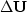 is a column vector containing the perturbation in the
wavefield at all depths,
is a column vector containing the perturbation in the
wavefield at all depths,
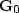 is a diagonal matrix containing the scattering term for
all the depth levels,
is a diagonal matrix containing the scattering term for
all the depth levels,
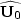 is a diagonal matrix containing the background wavefield
data for all the depth levels, and
is a diagonal matrix containing the background wavefield
data for all the depth levels, and
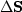 is a column vector containing the perturbation in the
velocity for all the depth levels.
is a column vector containing the perturbation in the
velocity for all the depth levels.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() and
and ![]() ).
).
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
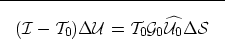
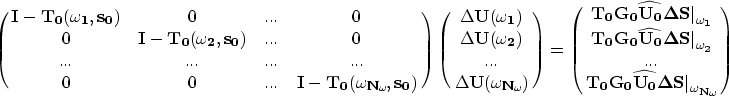
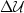 is a column vector containing the perturbation in the
wavefield for all the frequencies,
is a column vector containing the perturbation in the
wavefield for all the frequencies,
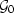 is a diagonal matrix containing the scattering operator
for all the frequencies,
is a diagonal matrix containing the scattering operator
for all the frequencies,
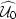 is a diagonal matrix containing the background wavefield
for all the frequencies, and
is a diagonal matrix containing the background wavefield
for all the frequencies, and
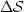 is a column vector containing the perturbation in slowness,
same for all the frequencies if we disregard dispersion.
is a column vector containing the perturbation in slowness,
same for all the frequencies if we disregard dispersion.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() and
and ![]() ).
).
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() )
as a function of the perturbation in slowness (
)
as a function of the perturbation in slowness (![]() ) like this:
) like this:
![]() ),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies (
),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies (![]() ):
):
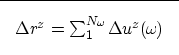

![]() ), corresponding to the
perturbation velocity field (
), corresponding to the
perturbation velocity field (![]() ), can be computed as follows:
), can be computed as follows: