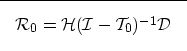Downward continuation
The first step of migration consists of downward continuation of the wavefield
measured at the surface (a.k.a. the data), which is done by the recursive
application of the equation:
| 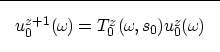 |
(10) |
initialized by the wavefield at the surface, as follows:
| 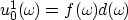 |
(11) |
where
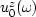 is the wavefield
is the wavefield 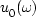 at depth z,
at depth z,
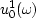 is the wavefield
is the wavefield 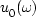 at the surface z=0,
at the surface z=0,
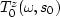 is the downward continuation operator at depth z,
is the downward continuation operator at depth z,
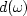 is the data, i.e.. the wavefield at the surface, and
is the data, i.e.. the wavefield at the surface, and
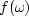 is a frequency-dependent scale factor for the data.
is a frequency-dependent scale factor for the data.
The recursion in Equations (A-1) and (A-2) can
be also rewritten in matrix form as
| ![\begin{displaymath}
\fbox {$
[\bf {I}-\bf {T_0}]\bf{U_0}=\bf {D}
$}
\end{displaymath}](img33.gif) |
(12) |
where
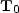 is a square matrix containing the downward continuation
operator for all depth levels,
is a square matrix containing the downward continuation
operator for all depth levels,
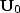 is a column vector containing the wavefield at all depth
levels, and
is a column vector containing the wavefield at all depth
levels, and
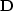 is a column vector containing the scaled
data.
is a column vector containing the scaled
data.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Equation (A-3) represents the downward continuation
recursion written for a given frequency. We can write a similar
relationship for each of the frequencies in the analyzed data, and
group them all in the matrix relationship
| 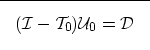 |
(13) |
where
 is a diagonal matrix containing the downward continuation
operators for all the frequencies in the data,
is a diagonal matrix containing the downward continuation
operators for all the frequencies in the data,
 is a column vector containing the wavefield data for all
the frequencies, and
is a column vector containing the wavefield data for all
the frequencies, and
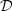 is a column vector containing the scaled data at all
frequencies.
is a column vector containing the scaled data at all
frequencies.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
It follows from Equation (A-4) that the background
wavefield (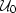 ) can be computed as a function of the measured data
(
) can be computed as a function of the measured data
(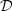 ), as follows:
), as follows:
| 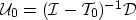 |
(14) |
Imaging
The second step of the migration by downward continuation is imaging. In
the exploding reflector concept, the image is found by selecting the
wavefield at time t=0 or, equivalently, by summing over the
frequencies  :
:
| 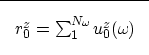 |
(15) |
where
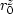 is the image (reflectivity) corresponding to a given
depth level z.
is the image (reflectivity) corresponding to a given
depth level z.
We can write the Equation (A-6) in matrix form as
| 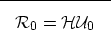 |
(16) |
where
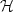 is an operator performing the summation over frequency for
every depth level z, and
is an operator performing the summation over frequency for
every depth level z, and
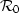 is a column vector containing the image at every depth
level.
is a column vector containing the image at every depth
level.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
Therefore, the image (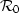 ), corresponding to the background velocity
field, can be computed from the measured data (
), corresponding to the background velocity
field, can be computed from the measured data (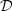 ) using the summation
(
) using the summation
(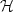 ) and the downward continuation operators (
) and the downward continuation operators (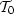 ) as
) as
| 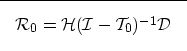 |
(17) |
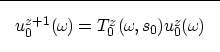
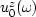 is the wavefield
is the wavefield 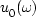 at depth z,
at depth z,
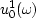 is the wavefield
is the wavefield 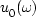 at the surface z=0,
at the surface z=0,
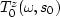 is the downward continuation operator at depth z,
is the downward continuation operator at depth z,
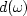 is the data, i.e.. the wavefield at the surface, and
is the data, i.e.. the wavefield at the surface, and
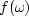 is a frequency-dependent scale factor for the data.
is a frequency-dependent scale factor for the data.
![\begin{displaymath}
\fbox {$
[\bf {I}-\bf {T_0}]\bf{U_0}=\bf {D}
$}
\end{displaymath}](img33.gif)
![\begin{eqnarray}
\left[ \matrix {
{1} & 0 & 0 &...& 0 & 0 \cr
{-T_0^{1}} & {1} &...
...left[ \matrix{
f~d \cr 0 \cr 0 \cr...\cr 0 \cr
} \right]\nonumber \end{eqnarray}](img34.gif)
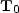 is a square matrix containing the downward continuation
operator for all depth levels,
is a square matrix containing the downward continuation
operator for all depth levels,
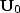 is a column vector containing the wavefield at all depth
levels, and
is a column vector containing the wavefield at all depth
levels, and
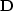 is a column vector containing the scaled
data.
is a column vector containing the scaled
data.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
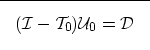
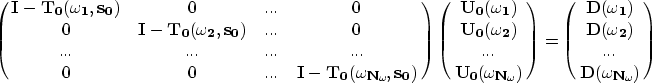
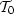 is a diagonal matrix containing the downward continuation
operators for all the frequencies in the data,
is a diagonal matrix containing the downward continuation
operators for all the frequencies in the data,
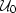 is a column vector containing the wavefield data for all
the frequencies, and
is a column vector containing the wavefield data for all
the frequencies, and
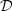 is a column vector containing the scaled data at all
frequencies.
is a column vector containing the scaled data at all
frequencies.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() ) can be computed as a function of the measured data
(
) can be computed as a function of the measured data
(![]() ), as follows:
), as follows:
![]() :
:
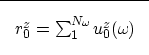
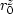 is the image (reflectivity) corresponding to a given
depth level z.
is the image (reflectivity) corresponding to a given
depth level z.
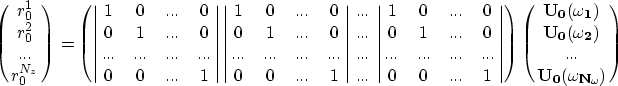
 is an operator performing the summation over frequency for
every depth level z, and
is an operator performing the summation over frequency for
every depth level z, and
 is a column vector containing the image at every depth
level.
is a column vector containing the image at every depth
level.
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
![]() ), corresponding to the background velocity
field, can be computed from the measured data (
), corresponding to the background velocity
field, can be computed from the measured data (![]() ) using the summation
(
) using the summation
(![]() ) and the downward continuation operators (
) and the downward continuation operators (![]() ) as
) as