




Next: Admissible Models
Up: Symes: Differential semblance
Previous: Error, Error Everywhere!
The linearized model accurately predicts only precritical primary
reflections. For layered media, precritical reflections have downgoing
incident rays. Along downgoing rays, time is an increasing function
of depth. It follows that if t0 is to be a depth variable, then T
must be an increasing function of t0. This is generally true only
in a subset of the t,x plane, i.e. only part of this plane contains
data accurately modeled by linearized acoustics. Therefore the rest of
the data must be muted out.
Define the stretch factor
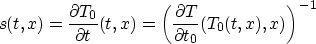
Then the condition that T(t0,x) be monotone increasing as a
function of t0 is equivalent to demanding that for large enough t
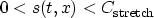
where 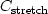 is a user-specified parameter larger than one.
Define
is a user-specified parameter larger than one.
Define 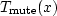 (the mute boundary)
to be the infimum of all t for which the
above inequality is satisfied on the interval
(the mute boundary)
to be the infimum of all t for which the
above inequality is satisfied on the interval 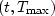 . Then
the support of the mute function
. Then
the support of the mute function 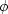 should be contained in the
set
should be contained in the
set 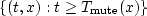 .
.
Define a corresponding t0,x domain mute by 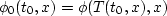 .
.





Next: Admissible Models
Up: Symes: Differential semblance
Previous: Error, Error Everywhere!
Stanford Exploration Project
4/20/1999
![]()
![]()
![]() .
.