




Next: Noise: General Case
Up: Symes: Differential semblance
Previous: Hyperbolic Moveout
Until further notice regard F etc. as depending on RMS square
slowness u rather than on interval velocity v. Dependence on v,
through the relatively easily analyzed map  , will be
reintroduced at the end.
, will be
reintroduced at the end.
A short calculation shows that
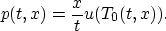
Introduce the quantity 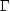 , with units of time:
, with units of time:
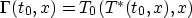
That is, 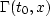 is the zero offset time for which the time at offset
x is the same in the slowness u as the time one obtains for t0,x in
slowness u*.
is the zero offset time for which the time at offset
x is the same in the slowness u as the time one obtains for t0,x in
slowness u*.
Then introducing the expression for p, and changing variables from t to
t0 in the integral above, yields
![\begin{displaymath}
J_0[u]=\int\int \,dt_0\,dx\,B_0(t_0,x)(u(\Gamma(t_0,x))-u^*(t_0))^2 (r^*(t_0))^2 + O(\lambda)\end{displaymath}](img82.gif)
where
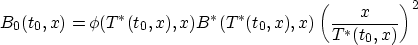
depends only on u* and 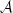 .
.
It is now straightforward to compute the first order perturbation
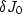 of J0 with respect to u. First,
of J0 with respect to u. First,
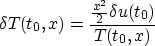
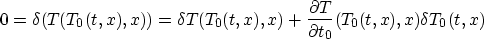
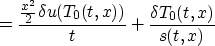
so
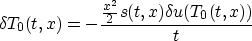
whence
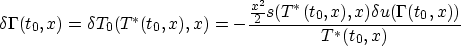
and
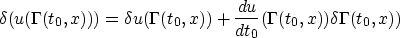
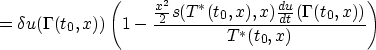
Recall that
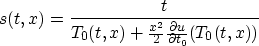
so that
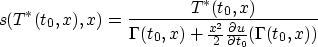
so
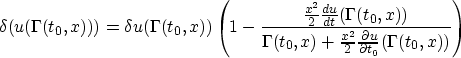
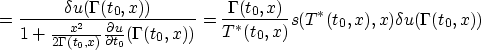
Putting this all together,
![\begin{displaymath}
\delta J_0[u]= \int\int \,dt_0\,dx\,B_1(t_0,x)(u(\Gamma(t_0,x))-u^*(t_0)) (r^*(t_0))^2\delta u(\Gamma(t_0,x)) + O(\lambda)\end{displaymath}](img96.gif)
where
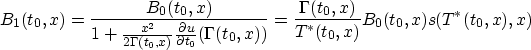
depends on u, u*, and  .To compute the gradient, change variables again to
.To compute the gradient, change variables again to 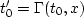 for
each x. Since
for
each x. Since
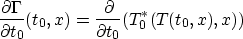
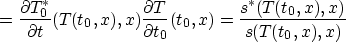
and so
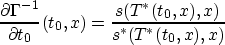
you get
![\begin{displaymath}
\delta J_0[u]= \int\int \,dt_0\,dx\,B_1^*(t_0,x)(u(t_0)-u^*(...
...t_0,x))) (r^*(\Gamma^{-1}(t_0,x)))^2\delta u(t_0)) + O(\lambda)\end{displaymath}](img102.gif)
with
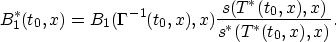
Thus the L2 gradient of J0 is
 = \int \,dx\,B_1^*(t_0,x)(u(t_0)-u^*(\Gamma^{-1}(t_0,x))) (r^*(\Gamma^{-1}(t_0,x)))^2 + O(\lambda)\end{displaymath}](img104.gif)
Both expressions for J0 and its gradient suggest that these quantities are
comparing the trial square slowness u and the target square slowness u* at
different points (eg. t0 vs. 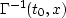 ), and this in turn makes
understanding of the implications for determination of u difficult.
Fortunately this is not really the case:
), and this in turn makes
understanding of the implications for determination of u difficult.
Fortunately this is not really the case:
Key Lemma: There exists a function h(t0,x), depending
on velocity v (or slowness u) and also on u* and 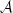 , having
the following properties:
, having
the following properties:
- h(t0,x)>0 over the mute zone, and
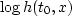 is uniformly
bounded for t0,x in the mute zone and
is uniformly
bounded for t0,x in the mute zone and 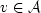 ;
; -
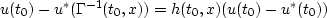
Proof of Key Lemma: Note first that since
T*(T*0(t,x),x)=t
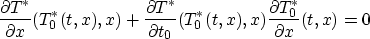
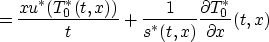
so
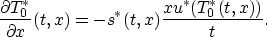
It follows that since
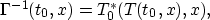
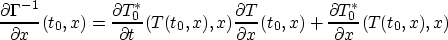
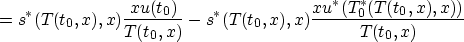
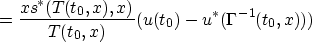
Thus
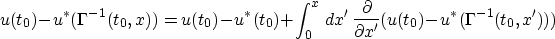
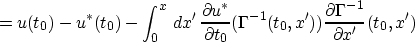
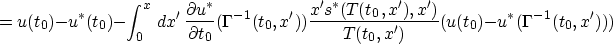
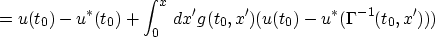
where
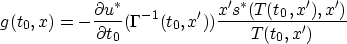
This simple integral equation has the solution
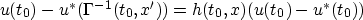
where
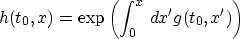
has the properties claimed for it in the statement of the lemma. Q.E.D.
Now changing variables in the asymptotic formula for J0, and
applying the above relation to both this and the formula for
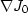 , you obtain
, you obtain
![\begin{displaymath}
J_0[u]=\int\int \,dt_0(u(t_0)-u^*(t_0))^2 \,dx\,B^*_0(t_0,x)h(t_0,x)(r^*(\Gamma^{-1}(t_0,x)))^2 + O(\lambda)\end{displaymath}](img123.gif)
 = (u(t_0)-u^*(t_0)) \int \,dx\,B_1^*(t_0,x)h(t_0,x)(r^*(\Gamma^{-1}(t_0,x)))^2 + O(\lambda)\end{displaymath}](img124.gif)
where
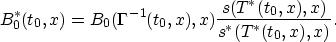
Now B0* and B1* differ at each point in the mute zone by factors or
divisors of s, s*, T, and the like, and these are bounded over the mute
zone uniformly in 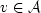 . Therefore there exists a constant C>0
depending only on
. Therefore there exists a constant C>0
depending only on 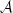 for which
for which
![\begin{displaymath}
J_0[u] \le C \int\, dt_0\, (u(t_0)-u^*(t_0))\nabla J_0[u](t_0) + O(\lambda)\end{displaymath}](img126.gif)
and we have proved the
Theorem: If u, the RMS square slowness for 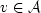 ,is a stationary point of J0[u], then
,is a stationary point of J0[u], then ![$J_0[u] = O(\lambda)$](img127.gif) .
.
That is, for noise free data, any stationary point of J0 is a
global minimizer, up to an asymptotically vanishing error.





Next: Noise: General Case
Up: Symes: Differential semblance
Previous: Hyperbolic Moveout
Stanford Exploration Project
4/20/1999
![]() , will be
reintroduced at the end.
, will be
reintroduced at the end.
![]()
![]()
![]()
![]()
![]() of J0 with respect to u. First,
of J0 with respect to u. First,
![]()
![]()
![]()
![]()
![]()
![]()
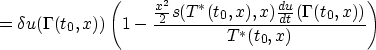
![]()
![]()
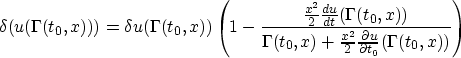
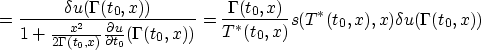
![]()
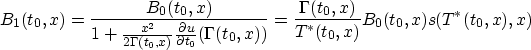
![]()
![]()
![]()
![]()
![]()
![]()
![]() , having
the following properties:
, having
the following properties:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , you obtain
, you obtain
![]()
![]()
![]()
![]()
![]() ,is a stationary point of J0[u], then
,is a stationary point of J0[u], then ![]() .
.