




Next: Deconvolution Examples
Up: Symes: Extremal regularization
Previous: Quadratically Constrained Quadratic Minimization
For arbitrary , denote by 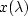 the solution
of the normal equations
the solution
of the normal equations
Set
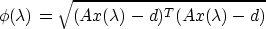
The secular equation is
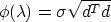
and its solution, if it has one, gives the correct value of the
Lagrange multiplier 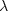 .
.
The Moré-Hebden algorithm takes its cue from the simplest possible
case: x and d are one-dimensional, and A and R are scalars.
In that very special case,
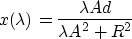
hence
i.e. the reciprocal of 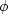 is a linear function of
is a linear function of 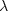 .This suggests that Newtons's method is more likely to converge
quickly when applied to
.This suggests that Newtons's method is more likely to converge
quickly when applied to
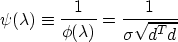
and that is exactly what the Moré-Hebden algorithm does.
The iteration proceeds as follows:
in which 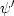 stands for the deriviative of
stands for the deriviative of 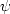 , which you compute
like so:
, which you compute
like so:
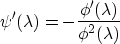
Now
From the normal equations,
so
Putting all of this together, one obtains the following algorithm for
updating 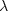 :
The first and third steps involve solution of linear systems, which
in geophysical applications may be very large. Therefore, in contrast
to conventional implementations of this algorithm, I use conjugate
gradient iteration Björk (1997) to compute the solutions of these
systems. As one might expect, the error reduction attained by these
inner iterations affects the overall convergence rate of the algorithm.
:
The first and third steps involve solution of linear systems, which
in geophysical applications may be very large. Therefore, in contrast
to conventional implementations of this algorithm, I use conjugate
gradient iteration Björk (1997) to compute the solutions of these
systems. As one might expect, the error reduction attained by these
inner iterations affects the overall convergence rate of the algorithm.
A final detail: since 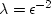 must remain positive, I have replaced any large
decrease implied by the above formula by a bisection strategy. Since
must remain positive, I have replaced any large
decrease implied by the above formula by a bisection strategy. Since
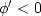 , as soon as
, as soon as 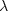 is too small (which forces the
weight onto the regularization term and increases the residual), the
algorithm produces regular increases in
is too small (which forces the
weight onto the regularization term and increases the residual), the
algorithm produces regular increases in 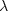 and converges very
rapidly, usually in one or two steps, so long as the normal equations
are solved successfully. This is not always the case,
but failure to converge rapidly appears to signal large data
components associated with very small eigenvalues and is a sure sign
that the noise level estimate
and converges very
rapidly, usually in one or two steps, so long as the normal equations
are solved successfully. This is not always the case,
but failure to converge rapidly appears to signal large data
components associated with very small eigenvalues and is a sure sign
that the noise level estimate  has been chosen too small.
has been chosen too small.





Next: Deconvolution Examples
Up: Symes: Extremal regularization
Previous: Quadratically Constrained Quadratic Minimization
Stanford Exploration Project
4/20/1999
![]() the solution
of the normal equations
the solution
of the normal equations
![]()
![]()
![]()
![]()
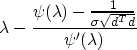
![]()
![]() must remain positive, I have replaced any large
decrease implied by the above formula by a bisection strategy. Since
must remain positive, I have replaced any large
decrease implied by the above formula by a bisection strategy. Since
![]() , as soon as
, as soon as ![]() is too small (which forces the
weight onto the regularization term and increases the residual), the
algorithm produces regular increases in
is too small (which forces the
weight onto the regularization term and increases the residual), the
algorithm produces regular increases in ![]() and converges very
rapidly, usually in one or two steps, so long as the normal equations
are solved successfully. This is not always the case,
but failure to converge rapidly appears to signal large data
components associated with very small eigenvalues and is a sure sign
that the noise level estimate
and converges very
rapidly, usually in one or two steps, so long as the normal equations
are solved successfully. This is not always the case,
but failure to converge rapidly appears to signal large data
components associated with very small eigenvalues and is a sure sign
that the noise level estimate ![]() has been chosen too small.
has been chosen too small.