




Next: Synthetic data tests
Up: Guitton & Symes: The
Previous: Introduction
The velocity domain representation of seismic data is an alternative to the standard
CMP presentation. Transformation of CMP data into the velocity domain (producing a velocity
model or panel of the data) exhibits clearly the moveout inherent in the data and therefore,
forms a convenient basis for velocity analysis as a linear inverse problem.
The velocity transform A from the model space (velocity domain)
into the data space (CMP gathers) stretches the velocities back
in the offset plane (superposition of hyperbolas) whereas the adjoint operation (A')
squeezes the data (summation over hyperbolas):
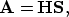
with
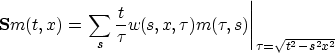
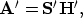
with
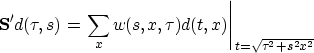
where 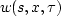 is a weighting function,
is a weighting function,  is a filter that we define later.
is a filter that we define later.
 is related to the velocity stack as defined by Taner and Koehler (1969).
is related to the velocity stack as defined by Taner and Koehler (1969).
The problem is: given a CMP gather can we find a velocity panel which synthesizes it 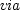
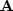 ? In equations, given data
? In equations, given data 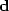 , we want to solve for model
, we want to solve for model  :
:
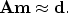
A simple way to solve this problem is to find a model  that minimizes the mean
square misfit
that minimizes the mean
square misfit
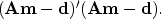
This optimization problem is equivalent to the linear system
(``normal equations'')
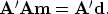
This system is easy to solve if 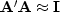 , i.e if
, i.e if 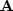 is close
to unitary: then
is close
to unitary: then 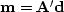 .In general,
.In general, 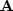 is far from an unitary operator for many reasons.
However, the choice of a weighting function compensates to some extent for
geometrical spreading and other effects Claerbout and Black (1997):
is far from an unitary operator for many reasons.
However, the choice of a weighting function compensates to some extent for
geometrical spreading and other effects Claerbout and Black (1997):
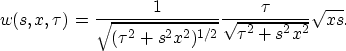
The summation in the velocity space boosts low frequencies. Claerbout and Black (1997) suggest that a good choice
of filter 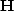 is a half derivative operator (
is a half derivative operator (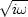 ).
These choices for
).
These choices for 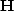 and
and 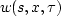 bring
bring 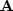 closer to being
an unitary operator.
closer to being
an unitary operator.
Since the data is noisy, the modeling operator is not unitary and the numbers of equations
and unknowns may be large, an iterative data-fitting approach seems reasonable:
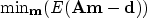
where  is the model,
is the model, 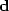 , the data we want to fit,
, the data we want to fit, 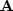 the modeling operator,
and E a misfit measurement function we have to choose.
We have already presented one possibility, namely that E is the l2 norm (least squares inversion).
A convenient iterative method in this case is to solve the normal equation using conjugate gradient iteration.
We refer to this approach as ``CG'' or ``l2''. An alternative approach is to take for E the Huber function
introduced in the first section. With this Huber misfit measure, the velocity transform inverse problem is no
longer equivalent to a linear system. We choose to solve it using a general-purpose nonlinear
optimizer, as mentioned above, rather than one of several special-purpose methods invented for this
type of problem. We refer to this approach as''Huber'' or the ``Huber solver''.
the modeling operator,
and E a misfit measurement function we have to choose.
We have already presented one possibility, namely that E is the l2 norm (least squares inversion).
A convenient iterative method in this case is to solve the normal equation using conjugate gradient iteration.
We refer to this approach as ``CG'' or ``l2''. An alternative approach is to take for E the Huber function
introduced in the first section. With this Huber misfit measure, the velocity transform inverse problem is no
longer equivalent to a linear system. We choose to solve it using a general-purpose nonlinear
optimizer, as mentioned above, rather than one of several special-purpose methods invented for this
type of problem. We refer to this approach as''Huber'' or the ``Huber solver''.
The next two parts of this paper compare the performance of the CG algorithm to Huber in
the velocity analysis application.





Next: Synthetic data tests
Up: Guitton & Symes: The
Previous: Introduction
Stanford Exploration Project
4/20/1999
![]()
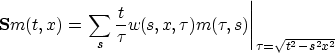
![]()
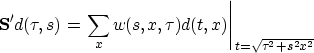
![]()
![]() ? In equations, given data
? In equations, given data ![]() , we want to solve for model
, we want to solve for model ![]() :
:![]()
![]()
![]()
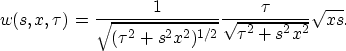
![]()