




Next: Understanding CG magic and
Up: THE WORLD OF CONJUGATE
Previous: Coding nonlinear fitting problems
The conjugate-direction method is really a family of methods.
Mathematically, where there are n unknowns, these algorithms all
converge to the answer in n (or fewer) steps. The various methods
differ in numerical accuracy, treatment of underdetermined systems,
accuracy in treating ill-conditioned systems, space requirements, and
numbers of dot products. Technically, the method of CD used in the
cgstep module ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can download
.
is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can download
.
I suggest you skip over the remainder of this section and return
after you have seen many examples and have developed some expertise,
and have some technical problems.
The conjugate-gradient method was introduced
by Hestenes and Stiefel in 1952.
To read the standard literature and relate it to this book,
you should first realize that when I write fitting goals like
| 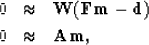 |
(84) |
| (85) |
they are equivalent to minimizing the quadratic form:
| 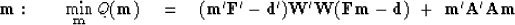 |
(86) |
The optimization theory (OT) literature starts from a minimization of
| 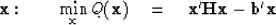 |
(87) |
To relate equation (86) to (87)
we expand the parentheses in (86)
and abandon the constant term 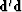 .Then gather the quadratic term in
.Then gather the quadratic term in 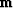 and the linear term in
and the linear term in 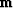 .There are two terms linear in
.There are two terms linear in 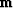 that are transposes of each other.
They are scalars so they are equal.
Thus, to invoke ``standard methods,'' you take
your problem-formulation operators
that are transposes of each other.
They are scalars so they are equal.
Thus, to invoke ``standard methods,'' you take
your problem-formulation operators 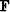 ,
, 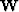 ,
, 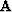 and create two subroutines that apply:
and create two subroutines that apply:
| 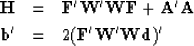 |
(88) |
| (89) |
The operators 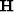 and
and 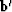 operate on model space.
Standard procedures do not require their adjoints
because
operate on model space.
Standard procedures do not require their adjoints
because 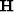 is its own adjoint and
is its own adjoint and 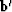 reduces model space to a scalar.
You can see that computing
reduces model space to a scalar.
You can see that computing 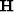 and
and 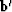 requires
one temporary space the size of data space
(whereas cgstep requires two).
requires
one temporary space the size of data space
(whereas cgstep requires two).
When people have trouble with conjugate gradients or conjugate
directions, I always refer them to the Paige and Saunders
algorithm LSQR. Methods that form 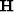 explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context. I
include module lsqr
explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context. I
include module lsqr ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) without explaining
why it works. The interface is similar to solver
without explaining
why it works. The interface is similar to solver
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Note that the residual vector does not appear
explicitly in the program and that we cannot start from a nonzero
initial model.
. Note that the residual vector does not appear
explicitly in the program and that we cannot start from a nonzero
initial model.
module lsqr {
logical, parameter, private :: T = .true., F = .false.
private :: normalize
contains
subroutine solver( oper, x, dat, niter) {
interface {
function oper( adj, add, x, dat) result (stat) {
integer :: stat
logical, intent( in) :: adj, add
real, dimension (:) :: x, dat
}
}
real, dimension (:), intent (in) :: dat
real, dimension (:), intent (out) :: x
integer, intent (in) :: niter
real, dimension ( size( x )) :: w, v
real, dimension ( size( dat)) :: u
integer :: iter, stat
double precision :: alfa, beta, rhobar, phibar
double precision :: c, s, teta, rho, phi, t1, t2
u = dat; x = 0. ; call normalize( u, beta)
stat = oper( T,F,v,u); call normalize( v, alfa)
w = v
rhobar = alfa
phibar = beta
do iter = 1, niter {
u = - alfa * u; stat = oper( F, T, v, u); call normalize( u, beta)
v = - beta * v; stat = oper( T, T, v, u); call normalize( v, alfa)
rho = sqrt( rhobar*rhobar + beta*beta)
c = rhobar/rho; s = beta/rho; teta = s * alfa
rhobar = - c * alfa; phi = c * phibar; phibar = s * phibar
t1 = phi/rho; t2 = -teta/rho
x = x + t1 * w
w = v + t2 * w
}
}
subroutine normalize( vector, size) {
real, dimension (:), intent (inout) :: vector
double precision, intent (out) :: size
size = sqrt( sum( dprod( vector, vector)))
vector = vector / size
}
}





Next: Understanding CG magic and
Up: THE WORLD OF CONJUGATE
Previous: Coding nonlinear fitting problems
Stanford Exploration Project
2/27/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can download
.
is not the
conjugate-gradient method itself, but is equivalent to it. This
method is more properly called the conjugate-direction method
with a memory of one step. I chose this method for its clarity and
flexibility. If you would like a free introduction and summary of
conjugate-gradient methods, I particularly recommend An
Introduction to Conjugate Gradient Method Without Agonizing Pain
by Jonathon Shewchuk, which you can download
.
![]() explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context. I
include module lsqr
explicitly or
implicitly (including both the standard literature and the book3
method) square the condition number, that is, they are twice as
susceptible to rounding error as is LSQR. The Paige and
Saunders method is reviewed by Nolet in a geophysical context. I
include module lsqr ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) without explaining
why it works. The interface is similar to solver
without explaining
why it works. The interface is similar to solver
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Note that the residual vector does not appear
explicitly in the program and that we cannot start from a nonzero
initial model.
. Note that the residual vector does not appear
explicitly in the program and that we cannot start from a nonzero
initial model.