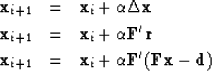
When we use the steepest-descent method, we iteratively find solutions by this updating:
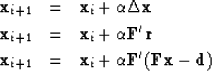 |
(50) | |
| (51) | ||
| (52) |
Suppose that by adding a huge amount of ![]() ,we now change
,we now change ![]() and continue iterating.
Notice that
and continue iterating.
Notice that ![]() remains zero
because
remains zero
because ![]() vanishes.
Thus we conclude that any null space in the initial guess
vanishes.
Thus we conclude that any null space in the initial guess ![]() will remain there unaffected by the gradient-descent process.
will remain there unaffected by the gradient-descent process.
Although finding a basis for the null space would take
us too far afield into linear algebra,
a more practical goal is to see some members of the null space, if any.
To try to see a member of the null space,
we take two starting guesses
and run our iterative solver for each of them.
If the solutions are the same, there is no null space.
If the two different solutions differ,
say ![]() and
and ![]() , there will be a null space.
Since the residual squared is a convex quadratic function,
the two solutions must have the same residual
, there will be a null space.
Since the residual squared is a convex quadratic function,
the two solutions must have the same residual ![]() .Subtracting
.Subtracting
![]() from
from
![]() we find
we find
![]() ,so
,so ![]() is a model in the null space.
Adding
is a model in the null space.
Adding ![]() to any to any model
to any to any model ![]() will not change the theoretical data.
will not change the theoretical data.
|
A practical way to learn about the existence of null spaces and their general appearance is simply to try gradient-descent methods beginning from various different starting guesses. |