|
|
|
|
Two point raytracing for reflection off a 3D plane |
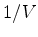 seconds.
This makes a traveltime of 1 glorp correspond to 1 meter of travel distance.
seconds.
This makes a traveltime of 1 glorp correspond to 1 meter of travel distance.
I make life simpler by observing that the traveltime gradient has the same azimuth as the reflector's dip azimuth. This must be so because translating the source-receiver pair along strike does not change the reflection arrival time. I note that this does not say that the reflection point moves along the dip azimuth when the surface arrival point moves along the dip azimuth.
The next twist is that instead of translating the source-receiver pair along
the dip azimuth, I'll translate the reflector plane along its normal direction.
This implies that derivatives with respect to the reflector normal direction
need to be scaled by the sine of the reflector dip, i.e.
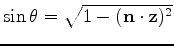 , as the surface intercept
of the reflector moves a distance inversely related to the sine of the dip.
Fortunately, even the zero dip case, where the reflector does not
intersect the surface,
is handled properly because the sine is zero in that case.
, as the surface intercept
of the reflector moves a distance inversely related to the sine of the dip.
Fortunately, even the zero dip case, where the reflector does not
intersect the surface,
is handled properly because the sine is zero in that case.
If we translate the initial reflection point 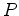 by
by
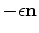 ,
where my convention for
,
where my convention for 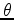 implies
implies
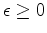 corresponds to a positive time slope, we
obtain a point on the displaced reflection plane, though generally not
the new reflection point
corresponds to a positive time slope, we
obtain a point on the displaced reflection plane, though generally not
the new reflection point 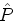 . The relation of
. The relation of 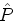 to
to 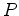 can be ascertained as before by dotting with
can be ascertained as before by dotting with 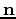 :
:
Continuing as before,
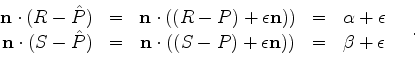
yielding
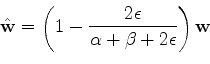
which says that
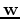 does not rotate.
does not rotate.
To compute changes in lengths (traveltimes), we have the relations
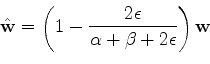
and
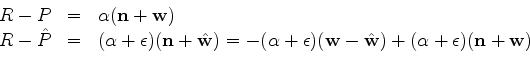
whence
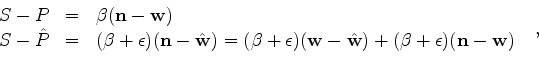
Taking first differences, we have
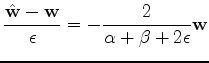
and
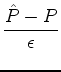 |
 |
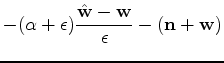 |
|
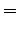 |
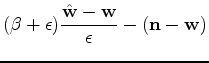 |
 |
 |
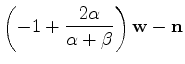 |
|
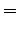 |
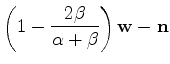 |
||
![$\displaystyle \makebox[0pt][r]{or, averaging the two,\ \ \ \ \ \ \ \ \ \ \ \/}$](img95.png) |
|||
 |
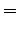 |
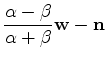 . . |
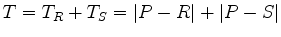
to get
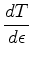 |
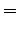 |
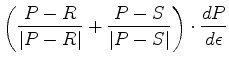 |
|
 |
 |
||
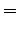 |
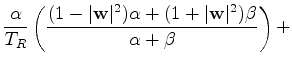 |
||
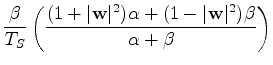 |
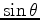 to obtain
the surface time slope.
to obtain
the surface time slope.
This last expression has a simple geometric meaning. As
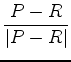 and
and 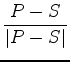
are unit vectors pointing towards the reflection point from the receiver and source respectively, their sum is necessarily parallel to their angle bisector, the normal. In particular, they sum to
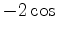
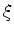
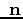 where
where
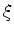 is the angle of incidence or reflection.
Dotting this with
is the angle of incidence or reflection.
Dotting this with
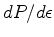 and multiplying by
and multiplying by
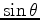 we
have that
the time slope is simply
we
have that
the time slope is simply
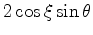 .
Changing units from glorps back to seconds, this agrees with the
well-known zero-offset result
.
Changing units from glorps back to seconds, this agrees with the
well-known zero-offset result
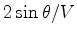 .
.
|
|
|
|
Two point raytracing for reflection off a 3D plane |