|
|
|
|
Two point raytracing for reflection off a 3D plane |
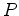 , on a planar subsurface
reflector will appear in a constant-offset, constant-azimuth survey.
, on a planar subsurface
reflector will appear in a constant-offset, constant-azimuth survey.
For this calculation, there is one fixed coordinate, the depth axis,
with the sources and receivers on the surface, described by
an arbitrary point 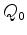 with (downward) normal
with (downward) normal 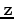 .
We are further
given the source-to-receiver offset vector
.
We are further
given the source-to-receiver offset vector 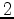
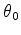
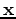 and the reflector inward normal
and the reflector inward normal 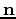 from the point
from the point 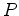 on the reflector.
on the reflector.
We know the ellipsoid of specular reflection has its major axis through
the source and receiver, and that the inward normal bisects the
reflection angle between the source and receiver. Therefore
the normal line through the reflection point intersects the
source-receiver axis somewhere between the source and receiver.
Let 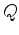 be the point on the surface where the normal ray would reach.
Then we may write
be the point on the surface where the normal ray would reach.
Then we may write
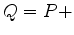
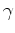
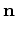
for some scalar
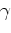 . As before we calculate
. As before we calculate
and the horizontal distance of
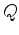 from the vertical plane through P as
from the vertical plane through P as
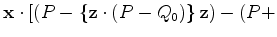
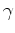
![$\displaystyle {\bf n}) ] =$](img43.png)
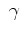
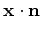
thereby fixing the source-receiver axis and the relative location of
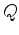 . What still remains is to
ascertain the source-receiver midpoint relative to
. What still remains is to
ascertain the source-receiver midpoint relative to 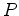 .
This we can determine by means
of tedious algebra, the way I did it, or by a succinct bit of trigonometry
provide by Daniel Kane (pers. comm.) of the Stanford Department of Mathematics.
.
This we can determine by means
of tedious algebra, the way I did it, or by a succinct bit of trigonometry
provide by Daniel Kane (pers. comm.) of the Stanford Department of Mathematics.
|
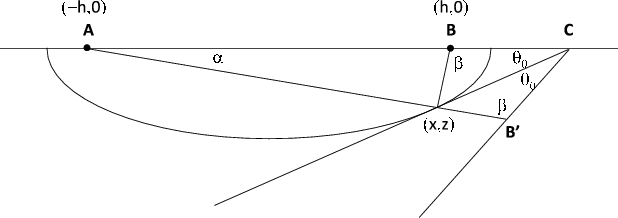
KaneProof
Figure 2. Diagram used to obtaining a quadratic relation for calculating 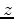 from
from 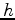 ,
, 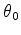 , and
, and  .
.
|
|
|---|---|
|
|
Due to symmetry, we may rotate the reflection point around the source-receiver
axis until it is directly below that axis. This does not change the
unknown distance to the source-receiver midpoint, but does reduce the
computation to one on a planar ellipse. Let 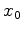 and
and 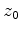 denote the respective horizontal and vertical distances
from the source-receiver midpoint to the reflection point.
The dip angle
denote the respective horizontal and vertical distances
from the source-receiver midpoint to the reflection point.
The dip angle  is implicitly determined by
is implicitly determined by
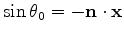 and
and
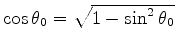 .
Using this dip angle,
.
Using this dip angle, 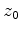 may be written as
may be written as
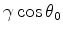 .
Referring
to Fig. 2, Fermat's principle of extremal traveltime
tells us that reflecting a focus of the ellipse around the
tangent produces an image point on the straight line connecting the
reflection point and the other focus. Hence we know that
.
Referring
to Fig. 2, Fermat's principle of extremal traveltime
tells us that reflecting a focus of the ellipse around the
tangent produces an image point on the straight line connecting the
reflection point and the other focus. Hence we know that 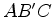 forms
a triangle. Denoting the three angles
forms
a triangle. Denoting the three angles
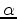 ,
, 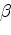 , and
, and  as illustrated in the figure, we have
as illustrated in the figure, we have
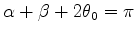
whence
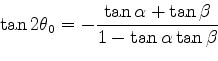 .
.
But
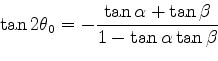
hence
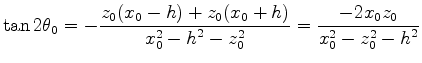
and so we have the quadratic relation
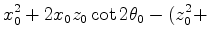
 .
.
Solving the quadratic equation we get
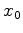 |
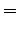 |
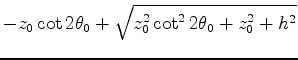 |
|
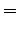 |
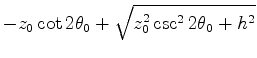 |
||
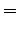 |
 |
||
 |
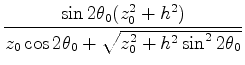 |
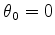 .
.
The relation
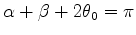 is actually a special
case of the more general proposition attributed to Boškovic (Boscovich) (1754):
is actually a special
case of the more general proposition attributed to Boškovic (Boscovich) (1754):
From any point  outside an ellipse with foci
outside an ellipse with foci  and
and 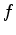 , with
, with
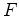 being no farther from
being no farther from 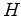 than
than 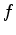 ,
draw two tangents, touching the ellipse at
,
draw two tangents, touching the ellipse at 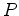 and
and 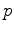 respectively.
Then the interior angle
respectively.
Then the interior angle 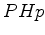 is half the difference of the
interior angles
is half the difference of the
interior angles 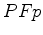 and
and 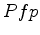 .
.
A translation of his original Latin demonstration appears in Appendix D.
So, in summary, only the dot products
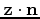 and
and
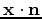 are
needed to find the demigration location of point
are
needed to find the demigration location of point 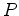 .
.
|
|
|
|
Two point raytracing for reflection off a 3D plane |