|
|
|
|
Two point raytracing for reflection off a 3D plane |
Formally, let the ray parameter 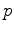 be in the open interval
be in the open interval
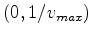 .
Starting from the origin, Snell's law
.
Starting from the origin, Snell's law
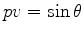 says that
says that
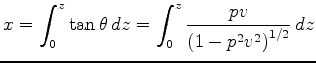
gives the horizontal displacement of the ray from the origin when it reaches depth
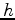 . Taking two derivatives of this formula
with respect to
. Taking two derivatives of this formula
with respect to 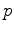 , we have
, we have
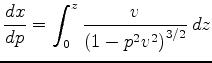 ,
, 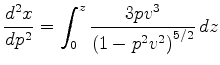 .
.
At a glance one sees that the second derivative is a quantity guaranteed to be positive in
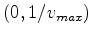 . By
Thorlund-Petersen (2004), Newton's method applied to finding the
. By
Thorlund-Petersen (2004), Newton's method applied to finding the 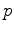 for
a ray that reaches a given
for
a ray that reaches a given 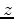 at given depth
at given depth 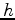 is therefore globally convergent. (Technically, we do need
to ensure that the Newton update doesn't overshoot the range
is therefore globally convergent. (Technically, we do need
to ensure that the Newton update doesn't overshoot the range
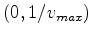 .)
.)
|
|
|
|
Two point raytracing for reflection off a 3D plane |