|
|
|
|
Two point raytracing for reflection off a 3D plane |
|
planerayfig
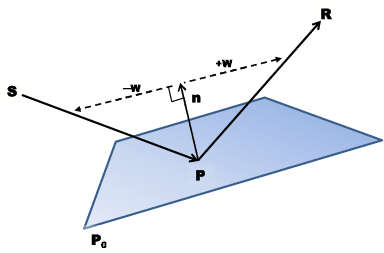
Figure 1. Diagram of planar reflector and the points and vectors I use for calculating the reflected raypath. |
|
|---|---|
|
|
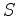 , a receiver location
, a receiver location 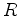 ,
and a plane
,
and a plane
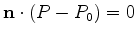 , where
, where
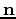 is a unit normal, to find the reflection point
is a unit normal, to find the reflection point 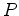 , drop
a perpendicular
, drop
a perpendicular 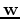 from
from 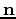 to the line connecting
to the line connecting 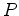 to
to 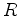 .
Snell's Law says that running
.
Snell's Law says that running 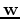 in the other direction connects
to the line between
in the other direction connects
to the line between 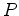 and
and 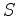 . So for some scalars
. So for some scalars 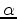 and
and 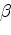 we have
we have
Dotting 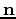 onto the first two equations gives
onto the first two equations gives
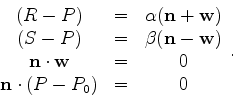
and subtracting the first two equations produces
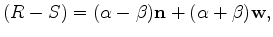
which can be solved directly for
 now that we have
now that we have  and
and 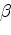 .
Given this
.
Given this 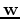 , the first equation immediately yields
, the first equation immediately yields
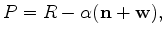
the desired reflection point. This can also be described in terms of the midpoint
 of the source and receiver as
of the source and receiver as
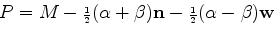 .
.
|
|
|
|
Two point raytracing for reflection off a 3D plane |