Decon in the log domain - practical considerations

Introduction

In marine streamer acquisition, both the source and the receivers are at some depth. As a result, their reflection from the water surface generates ``ghost'' arrivals. These ghosts are recorded in addition to the primary path of energy propagation from source to reflector to receiver. This causes the recordings of the specular reflections to be in practice non-minimum phase wavelets, and more similar to Ricker wavelets, as most of the energy does not arrive at the onset of the wavelet. Since Ricker is a delayed zero-phase wavelet, predictive decon will have limited success on marine streamer data, as the inverse filter will have coefficients that increase with time. Additionally, the airgun typically employed as a source in marine surveys generates a low-frequency bubble, whose reverberations contaminate the recorded data.

Zhang et al. (2011) extended traditional deconvolution to non-minimum phase wavelets. Claerbout et al. (2011) replaced the unknown filter coefficients by lag coefficients in the log spectrum of the deconvolution filter. Given data 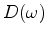$D(\omega)$ , the deconvolved output $r_t$ is:

$$r_t \ =\ {\rm FT}^{-1}\ \left[ D(\omega)\ \exp\left( \sum_t u_tZ^t \right) \right]$$ (1)

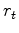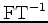where ${\rm FT}^{-1}$ is the inverse Fourier transform, and 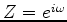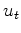$Z=e^{i\omega}$ . $u_t$ are the log spectrum variables of the deconvolution filter. The source wavelet is the inverse of the exponent of these log variables. The positive lag coefficients correspond to the causal part of the wavelet, and the negative ones to the anticausal part.

Claerbout et al. (2012) introduced the concept of inverting for sparsity, with the added complication that seismic data is non-stationary but decreases in amplitude over time. A gained residual 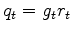$q_t = g_t r_t$ is sparsified using a hyperbolic penalty function 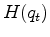$H(q_t)$ , where 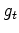$g_t$ is a known gain function. The inversion finds the model parameters 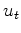$u_t$ which cause the gained residual 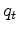$q_t$ to be as sparse as possible. The purpose is to enhance frequencies where they promote sparsity, which is our assumption about the underlying geology. In addition they proposed two regularizations:

Symmetry regularization
The expected shot waveform is a zero-phase Ricker wavelet, ignoring the bubble which arrives later. Therefore, in the log spectral domain it is desirable to have only even parts of the filter coefficients 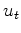$u_t$ around the zero-lag. The symmetry regularization does this by incorporating the odd parts near zero-lag into the residual:

$$0 \approx \epsilon_1 \sum_\tau w_\tau (u_\tau-u_{-\tau}),$$ (2)

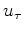where $u_\tau$ are the coefficients at positive lags and 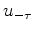$u_{-\tau}$ the coefficients at negative lags. 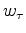$w_\tau$ is a weighting function that decreases from one to zero with increasing lag. Conceptually, the width of the weighting function should be just large enough to contain the Ricker wavelet of the data. 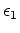$\epsilon_1$ controls the degree to which this regularization affects the objective function.

Filter length regularization
The deconvolution filter's positive lags should include both the zero-phase Ricker wavelet of the reflections, and the wavelet of the bubble with its reverberations (which are caused by the implosion of water into the cavity generated by the airgun). The filter should not have large negative lags, beyond those needed for the anti-causal part of the Ricker wavelet. Therefore a filter length lag regularization is added to the residual

$$0 \approx \epsilon_2 \sum_\tau \left( c_\tau u_\tau + a_{-\tau} u_{-\tau} \right),$$ (3)

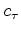where $c_\tau$ is the weighting function for the positive lags. This function starts at zero for small positive lags, until the lag deemed to be sufficient to contain the bubble. 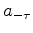$a_{-\tau}$ is the weighting function for the negative lags. This function is zero for small negative lags, and it ramps up from zero to one within a small time lag, since we do not expect anything before zero time other than the first lobe of the Ricker.

Decon in the log domain - practical considerations