|
|
|
|
Modeling data error during deconvolution |
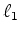 norm has well-known remarkable qualities.
Even more suitable to seismic problems is the hyperbolic penalty function
norm has well-known remarkable qualities.
Even more suitable to seismic problems is the hyperbolic penalty function
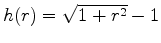 (Li et al. (2010)).
Applying it to deconvolution of 2-D synthetic data easily solved a complicated case not solveable by
(Li et al. (2010)).
Applying it to deconvolution of 2-D synthetic data easily solved a complicated case not solveable by  decons
(Zhang and Claerbout (2010a)).
Unfortunately, application to field data was not successful.
Returning to synthetic data, the culprit turned out to be the minimum-phase assumption.
This can be understood by examining the Ricker (non-minimum phase) wavelet,
a long-standing example of a wavelet hard to spike.
decons
(Zhang and Claerbout (2010a)).
Unfortunately, application to field data was not successful.
Returning to synthetic data, the culprit turned out to be the minimum-phase assumption.
This can be understood by examining the Ricker (non-minimum phase) wavelet,
a long-standing example of a wavelet hard to spike.
Solving for a product of forward and backward PEFs achieved an excellent result on synthetic data and a spectacular result on a Gulf of Mexico data set (Zhang and Claerbout (2010b)). By deconvolving properly we were delighted to find we had made reflection coefficient polarity much more clear. We were highly motivated to improve on this and integrate it with impedance estimation. Not well documented were difficulties connected with polarity reversal and apparent time shifts. They were attributed to the non-linearity of the method.
Claerbout et al. (2011) reformulated the problem in the frequency domain with the unknown parameters being the values at lags defining the log spectrum. This avoided many problems, but extensive testing by Qiang Fu and Yi Shen revealed reliability issues much like those identified by Zhang. For a long while we understood our difficulty to be a need for preconditioning to guide the non-linear problem closer to the desired solution. Suddenly we came to realize the problem is more like a null space, though not exactly that because of the nonlinearity. The apparent polarity reversals and time shifts resulted from spiking the first or the third lobe of the Ricker wavelet instead of consistently spiking the middle lobe. Claerbout (2012) resolved these problems by means of a regularization (called the Ricker regularization) that ensures Ricker-like wavelets. Unfortunately, like all regularizations, you can never be sure how much to add, leading to degraded results when you add too much.
Then the non commutivity of gain with filtering was theoretically resolved leading to small but noticable improvements (Claerbout et al. (2012)). Guitton and Claerbout (2012) also added a regularization term that penalizes long positive or negative lags of the filter. This penalty ensures that the estimated wavelet does not shift in masking areas that can be present in the gain function (i.e., preventing local minima).
With stability now under much better control
(we still need to experiment with strength of the regularizations)
we set out to demonstrate that sparse decon principles could
find natural cutoffs for high and low frequencies in data.
We seemed to be seeing frequencies dangerously close
to the 125Hz Nyquist on our available 4ms data so
we ordered and waited to obtain 2ms data to boost the Nyquist to 250 Hz.
Much to our horror (Guitton and Claerbout (2012)),
sparseness decon, like old fashioned  decon,
boosts energy up to near the new much higher Nyquist.
Also discovered in that paper is that our shot wavelets are picking up sea swell noise.
We do not wish to filter out sea swell as a preprocess
because we do not wish to lose low frequency information
that could be essential to impedance estimation.
Swell noise modeling has been done by Parrish (2005).
Subtracting such models should work better than filtering.
decon,
boosts energy up to near the new much higher Nyquist.
Also discovered in that paper is that our shot wavelets are picking up sea swell noise.
We do not wish to filter out sea swell as a preprocess
because we do not wish to lose low frequency information
that could be essential to impedance estimation.
Swell noise modeling has been done by Parrish (2005).
Subtracting such models should work better than filtering.
The formulation of this paper integrates sea swell modeling with our non minimum-phase, sparseness goaled, shot waveform estimation and data deconvolution. The experimental results mentioned above led to the theory you find here. What else might we find? We expect the noise to contain any bits of the data with non-typical spectra, both amplitude and phase. Besides the low-frequency sea swell, we might find the water bottom itself and its multiples contain the very high frequencies that we do not expect in waves that penetrate the earth.
|
|
|
|
Modeling data error during deconvolution |