|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |
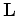 cannot model large time shifts
because the source function on the right-hand side of
equation 8 is triggered by the background wavefield
reaching a velocity perturbation,
and consequently it has the timing as the background wavefield.
Furthermore, the perturbed wavefield is propagated with the background
velocity
cannot model large time shifts
because the source function on the right-hand side of
equation 8 is triggered by the background wavefield
reaching a velocity perturbation,
and consequently it has the timing as the background wavefield.
Furthermore, the perturbed wavefield is propagated with the background
velocity
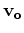 .
In mathematical terms
.
In mathematical terms
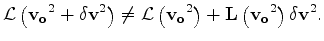 |
(9) |
The problem is even deeper.
When
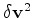 causes large time shifts by multiple
scattering,
there is no perturbation
causes large time shifts by multiple
scattering,
there is no perturbation
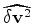 that can model those time shifts by single scattering;
that is,
that can model those time shifts by single scattering;
that is,
The non linearity of the modeling operator
makes the objective function
equation 2 to be non convex when
the velocity perturbations are sufficiently large.
Figure 1 shows an example of non-convexity of the
objective function.
The result correspond to several 1D transmission problems
sharing the same starting velocity (1.2 km/s)
and with different true velocities.
For all these experiments the source-receiver
offset is 4 km and the source function
is a zero-phase wavelet bandlimited between 5 and 20 Hz.
The FWI norm is plotted as a function of the true velocity.
If the true velocity is lower than
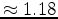 km/s
or larger than
km/s
or larger than
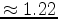 km/s a gradient based method
will not converge to the right solution,
even in this simple and low-dimensionality example.
km/s a gradient based method
will not converge to the right solution,
even in this simple and low-dimensionality example.
The challenges of solving the optimization problem
in equation 1 by gradient based optimization
can be alternatively represented by graphing,
as a function of the initial velocity error,
the search direction (opposite sign of the gradient direction)
of the objective function with respect to velocity square.
Figure 2 display this function computed
by applying the adjoint of the linear operator 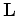 to the data residuals; that is
to the data residuals; that is
|
|
|
|
Tomographic full waveform inversion and linear modeling of multiple scattering |