|
|
|
|
Fast log-decon with a quasi-Newton solver |
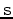 and
and 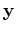 from the past
iterations, we update the Hessian using the information
from the
from the past
iterations, we update the Hessian using the information
from the 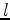 previous iterations, where
previous iterations, where 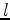 is given by the end-user.
This implies that when the number of iterations is smaller than
is given by the end-user.
This implies that when the number of iterations is smaller than 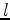 , we
have the usual BFGS update, and when it is larger than
, we
have the usual BFGS update, and when it is larger than 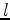 , we have
a limited-memory BFGS (L-BFGS) update.
, we have
a limited-memory BFGS (L-BFGS) update.
I give the updating formulas of the Hessian as presented by Nocedal (1980). First, we define
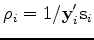 ,
, 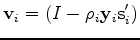 and
and 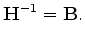
As described above, when
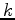 , the iteration number, obeys
, the iteration number, obeys
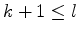 ,
where
,
where 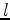 is the storage limit, we have the BFGS update
is the storage limit, we have the BFGS update
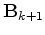 |
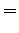 |
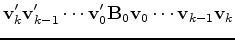 |
|
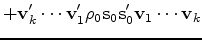 |
|||
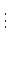 |
(4) | ||
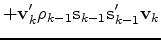 |
|||
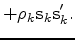 |
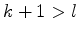 we have the limited-memory update
we have the limited-memory update
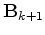 |
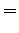 |
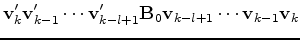 |
|
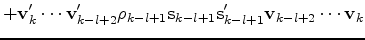 |
|||
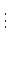 |
(5) | ||
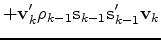 |
|||
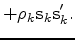 |
Usually the L-BFGS method is implemented with a line search for the
step length 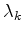 to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
to ensure a
sufficient decrease of the misfit function.
Convergence properties of the L-BFGS method are guaranteed if
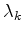 in equation (2) satisfies the Wolfe
conditions (Kelley, 1999):
in equation (2) satisfies the Wolfe
conditions (Kelley, 1999):
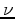 and
and 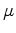 are constants to be chosen a priori and
are constants to be chosen a priori and
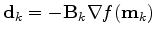 . For
. For 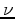 and
and 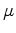 we set
we set 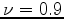 and
and
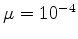 as proposed by
Liu and Nocedal (1989). Equation (6) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (7) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length
as proposed by
Liu and Nocedal (1989). Equation (6) is a
sufficient decrease condition that all line search algorithms must
satisfy. Equation (7) is a curvature condition. The
line search algorithm has to be carefully designed since it absorbs
most of the computing time. I programmed a line search based on the
More and Thuente (1994) method. Because the line search is time
consuming, the step length
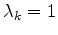 is always
tested first. This procedure saves a lot of computing time
and is also recommended by Liu and Nocedal (1989). I now give the
algorithm used to minimize any objective function involving nonlinear
problems.
is always
tested first. This procedure saves a lot of computing time
and is also recommended by Liu and Nocedal (1989). I now give the
algorithm used to minimize any objective function involving nonlinear
problems.
|
|
|
|
Fast log-decon with a quasi-Newton solver |