|
|
|
|
Fast log-decon with a quasi-Newton solver |
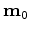 ,
, 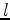 ,
,
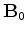 . Set
. Set 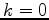 .
.
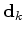 |
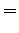 |
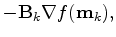 |
(8) |
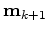 |
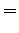 |
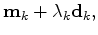 |
(9) |
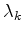 meets the Wolfe conditions.
meets the Wolfe conditions.
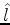 =min
=min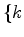 ,
, 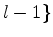 .
Update
.
Update
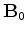
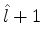 times using the pairs
times using the pairs
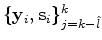 ,
i.e., let
,
i.e., let
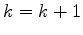 and go to 2 if the residual power is not small enough.
and go to 2 if the residual power is not small enough.
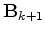 is not formed explicitly; instead we compute
is not formed explicitly; instead we compute
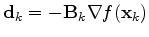 with an iterative formula
Nocedal (1980). Liu and Nocedal (1989) propose scaling the initial
symmetric positive definite
with an iterative formula
Nocedal (1980). Liu and Nocedal (1989) propose scaling the initial
symmetric positive definite
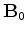 at each iteration as follows:
at each iteration as follows:
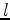 is
is 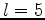 . In practice, the initial guess
. In practice, the initial guess
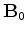 for the Hessian is the identity matrix
for the Hessian is the identity matrix  ;
then it might be scaled as proposed in equation (12). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer
;
then it might be scaled as proposed in equation (12). The
nonlinear solver as detailed in the previous algorithm converges to
a local minimizer
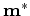 of
of
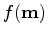 .
.
|
|
|
|
Fast log-decon with a quasi-Newton solver |