P/S separation of OBS data by inversion in a homogeneous medium

Wave mode separation and imaging

The Helmholtz separation operator is based on the assumption that any isotropic vector field can be described as a combination of a scalar and vector potential fields:

$$\mathbf u = \nabla \Phi + \nabla \times \mathbf \Psi,$$ (2)

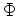where $\Phi$ is the scalar potential field and 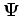$\mathbf \Psi$ is the vector potential. 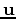$\mathbf u$ is the elastic displacement vector wavefield. The scalar potential generates pressure waves, and the vector potential generates shear waves. Therefore, the Helmholtz method of separating the P-wave amplitude from the S-wave amplitude is to apply a divergence operator and a curl operator to the displacement field:

$$P = \nabla \cdot \mathbf u = \nabla^2 \Phi;$$ (3)

$$\mathbf S = \nabla \times \mathbf u = -\nabla^2 \Psi.$$ (4)

Equations 3 and 4 apply only for an isotropic medium. Dellinger and Etgen (1990) extend these operators for an anisotropic medium.

The Helmholtz separation operator is useful for distinguishing between P and S-wave amplitudes, but it is not reversible. The derivation of a reversible P-wave and S-wave displacement decomposition by Zhang and McMechan (2010) is done in the wavenumber domain. They formulate a linear equation system based on characteristics of P and S particle displacements in an isotropic elastic medium. The solutions to this linear system in a two-dimensional medium are:

$$\tilde u^P_x = k^2_x \tilde u_x + k_x k_z \tilde u_z,$$ (5)

$$\tilde u^P_z = k^2_z \tilde u_z + k_z k_x \tilde u_x,$$ (6)

and

$$\tilde u^S_x = k^2_z \tilde u_x - k_x k_z \tilde u_z,$$ (7)

$$\tilde u^S_z = k^2_x \tilde u_z - k_z k_x \tilde u_x,$$ (8)

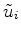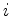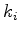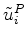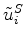where $\tilde u_i$ are the spatial fourier transforms of the observed displacement fields in direction $i$ , $k_i$ are the wavenumbers, and $\tilde u^P_i$ and $\tilde u^S_i$ are the decomposed P and S displacements. It is important to note that the 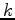$k$ in these equations is normalized by the absolute value of the wavenumber 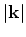$\left \vert \mathbf k \right \vert$ . This decomposition is reversible, since $u_i = u^P_i + u^S_i$ .

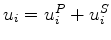P/S separation of OBS data by inversion in a homogeneous medium