 |
 |
 |
 | Hunting for microseismic reflections using multiplets |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Appendix A
Previous: Appendix A
Since S first arrivals are clearer and stronger than P first arrivals,
we use S arrivals to estimate a vector in the general direction of P arrivals.
The idea is to find the direction most perpendicular to the strongest
(direct) S arrivals.
We setup a
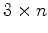 matrix of shear first arrivals,
matrix of shear first arrivals,
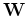 , by windowing around the first shear arrival.
As we seek a vector
, by windowing around the first shear arrival.
As we seek a vector 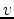 that is perpendicular
to the shear arrival direction (which is a P-arrival) we want
that is perpendicular
to the shear arrival direction (which is a P-arrival) we want
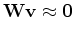 . . |
(1) |
We solve this by minimizing the objective function
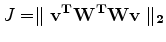 |
(2) |
subject to the constraint
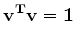 . . |
(3) |
Let 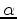 and
and 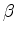 be two spherical surface coordinate parameters
over which we will minimize.
Taking partial derivatives of the constraints yields:
be two spherical surface coordinate parameters
over which we will minimize.
Taking partial derivatives of the constraints yields:
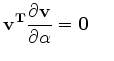 |
(4) |
and
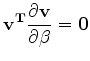 , , |
(5) |
which says that 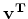 is perpendicular to the two partial derivatives.
Next, taking partial
derivatives of the sum of squares expression gives
is perpendicular to the two partial derivatives.
Next, taking partial
derivatives of the sum of squares expression gives
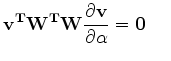 |
(6) |
and
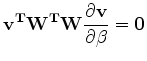 . . |
(7) |
Therefore
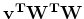 is also perpendicular to both
partial derivatives and consequently must
be parallel to
is also perpendicular to both
partial derivatives and consequently must
be parallel to 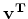 . This means that
. This means that
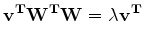 , , |
(8) |
where 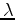 is the eigenvalue of the matrix
is the eigenvalue of the matrix
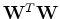 that will make the least squares expression a minimum.
Transposing we get
that will make the least squares expression a minimum.
Transposing we get
 , , |
(9) |
which is a classic eigenvector problem for the matrix
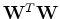 .
Since the right singular vectors of
.
Since the right singular vectors of 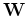 are the same as the eigenvectors of
are the same as the eigenvectors of
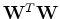 , we
used the LAPACK routine SGESVD to find our desired P-wave direction
vector.
, we
used the LAPACK routine SGESVD to find our desired P-wave direction
vector.
 |
 |
 |
 | Hunting for microseismic reflections using multiplets |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Appendix A
Previous: Appendix A
2012-05-10
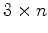 matrix of shear first arrivals,
matrix of shear first arrivals,
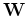 , by windowing around the first shear arrival.
As we seek a vector
, by windowing around the first shear arrival.
As we seek a vector 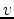 that is perpendicular
to the shear arrival direction (which is a P-arrival) we want
that is perpendicular
to the shear arrival direction (which is a P-arrival) we want
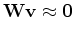 .
.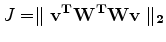
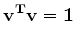 .
.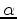 and
and 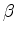 be two spherical surface coordinate parameters
over which we will minimize.
Taking partial derivatives of the constraints yields:
be two spherical surface coordinate parameters
over which we will minimize.
Taking partial derivatives of the constraints yields:
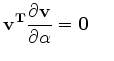
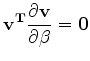 ,
,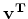 is perpendicular to the two partial derivatives.
Next, taking partial
derivatives of the sum of squares expression gives
is perpendicular to the two partial derivatives.
Next, taking partial
derivatives of the sum of squares expression gives
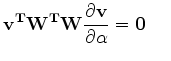
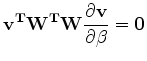 .
.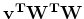 is also perpendicular to both
partial derivatives and consequently must
be parallel to
is also perpendicular to both
partial derivatives and consequently must
be parallel to 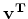 . This means that
. This means that
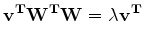 ,
,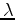 is the eigenvalue of the matrix
is the eigenvalue of the matrix
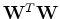 that will make the least squares expression a minimum.
Transposing we get
that will make the least squares expression a minimum.
Transposing we get
 ,
,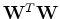 .
Since the right singular vectors of
.
Since the right singular vectors of 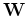 are the same as the eigenvectors of
are the same as the eigenvectors of
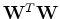 , we
used the LAPACK routine SGESVD to find our desired P-wave direction
vector.
, we
used the LAPACK routine SGESVD to find our desired P-wave direction
vector.