Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging

Production-induced Deformation

Realistic reservoir depletion exhibits asymmetric patterns that might be indicative of a complex reservoir geometry as well as spatial heterogeneity of the reservoir permeability. In particular, differences in production-related pressure change across multiple wells can help identify reservoir compartmentalization (Zoback, 2010) and guide the drilling of subsequent production wells, or affect the choice of production-enhancement techniques. In the general case of an arbitrary linear poroelastic medium, change in the pore pressure is intricately interconnected with the change in the stress field, and accurate modeling of the effects of changing pore pressure requires solving a system of governing equations in a half-space (Wang, 2000), (Segall, 2010). Solving a boundary-value problem for such a system of equations governing both stress evolution and fluid flow is challenging - as much due to uncertainty of the subsurface model parameters as due to the sheer analytical complexity of these coupled equations. The importance of studying the fully-coupled poroelastic models cannot be overestimated as the coupled modeling is often the key to explaining counterintuitive behaviour of some real-world poroelastic models.

In this work we expand on previous studies of the effects of pore pressure change on the strain and stress fields (Segall, 1992),(Segall et al., 1994) by adopting an intermediate approach between the fully coupled simulation and uncoupled analytical solutions. First, we assume that a pore pressure drop is known within the reservoir and is an arbitrary function of the reservoir coordinates - i.e., we assume partial fluid-to-solid coupling - and use the analytical expression for the elastostatic Green's tensor due to a concentrated centre of dilatation in half-space (Segall, 2010),(Mindlin, 1936) to numerically compute the displacement due to the pore pressure change. Next, we use the obtained numerical operator in an inversion problem, fitting a pore pressure drop to a known displacement and subsidence profile. Finally, we extend the method for layered media. The method is demonstrated on synthetic data based on a real-world example of subsidence due to the production from a hydrocarbon reservoir at Lacq, France (Segall et al., 1994). Extensions of this study to joint application with time-lapse seismic imaging are discussed as well. This paper is dedicated to reporting some geomechanical aspects of the joint geomechanics/seismic imaging effort aimed at applying the author's optimisation framework to problems of computational geophysics.

As a side note, apart from its potential application to the regularization of seismic inversion, numerical modeling of deformation due to changing pore pressure is one of the key problems of reservoir geomechanics (Zoback, 2010). Reservoir depletion has been demonstrated to have appreciable effect on stress both inside and outside of the producing reservoir (Zoback, 2010),(Geertsma, 1973),(Segall, 1992),(Segall et al., 1994),(Zoback and Zinke, 2002),(Segall and Fitzgerald, 1998). While some simplifying assumptions with regard to reservoir geometry (e.g., an infinitely wide and thin horizontal layer) yield a simple law for the horizontal stress change with the pressure decline within the reservoir (Zoback, 2010),(Segall and Fitzgerald, 1998)), estimating induced stress-field changes around the reservoir requires more elaborate models of reservoir depletion (Geertsma, 1973),(Segall, 1992). Simple disk-shaped and radially-symmetric reservoir shapes proved adequate for many simple situations, but compartmentalization and heterogeneous permeability inside realistic reservoirs point to a departure of the pore pressure decline from simple axisymmetric patterns (Zoback, 2010). Compartmentalization with impermeable barriers still allows for the application of a radially-symmetric pore pressure change law to individual reservoir compartments. However, an asymmetric pore pressure drop should be able to account for the effects of partial permeability or complex spatial geometry. Since a computationally-efficient technique for modeling and inverting asymmetric reservoir depletion patterns is an important by-product of our study, it is hoped that the computational tools and methods developed for this study will find independent application to the study of production-induced stressing and deformation.

reservoirdome Figure 1. Reservoir dome. The effective depth of the reservoir is 3.5km, effective radius 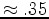$\approx 8$ km and width 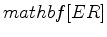$\approx .35$ km.

Identifying reservoir depletion patterns from production-induced deformations with applications to seismic imaging