|
|
|
|
Decon in the log domain with variable gain |
Having data 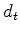 , having chosen gain
, having chosen gain 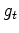 ,
and having a starting log filter, say
,
and having a starting log filter, say 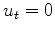 ,
let us see how to update
,
let us see how to update 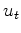 to find a gained output
to find a gained output
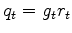 with better hyperbolicity.
Our forward modeling operation with model parameters
with better hyperbolicity.
Our forward modeling operation with model parameters 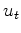 acting upon data
acting upon data 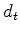 (in the Fourier domain
(in the Fourier domain 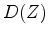 where
where
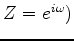 produces deconvolved data
produces deconvolved data 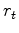 (the residual).
(the residual).
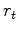 |
 |
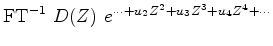 |
(9) |
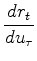 |
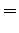 |
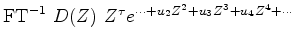 |
(10) |
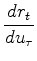 |
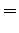 |
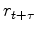 |
(11) |
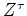 shifts the data
shifts the data 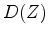 by
by 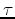 units
which shifts the residual the same amount.
Output formerly at time
units
which shifts the residual the same amount.
Output formerly at time 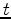 moves to time
moves to time 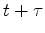 .
This is not the familiar result that the derivative of
an output with respect to a filter coefficient at lag
.
This is not the familiar result that the derivative of
an output with respect to a filter coefficient at lag 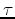 is the shifted input
is the shifted input
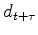 .
Here we have the output
.
Here we have the output
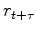 .
This difference leads to remarkable consequences below.
.
This difference leads to remarkable consequences below.
It is the gained residual
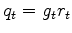 that we are trying to sparsify.
So we need its derivative by the model parameters
that we are trying to sparsify.
So we need its derivative by the model parameters 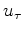 .
.
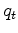 |
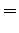 |
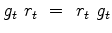 |
(12) |
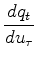 |
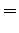 |
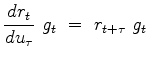 |
(13) |
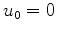 and hence
and hence
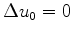 .
To find the update direction at nonzero lags
.
To find the update direction at nonzero lags
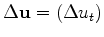 take the derivative of the hyperbolic penalty function
take the derivative of the hyperbolic penalty function
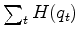 by
by 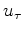 .
.
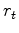 with the statistical residual
with the statistical residual
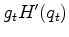 .
Notice in reflection seismology the physical residual
.
Notice in reflection seismology the physical residual 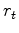 generally decreases with time
while the gain
generally decreases with time
while the gain 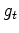 generally increases to keep the statistical variable
generally increases to keep the statistical variable 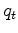 roughly constant,
so
roughly constant,
so
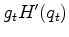 grows in time(!)
grows in time(!)
In the frequency domain
the crosscorrelation
(16) is:
Equation (17) is wrong at 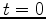 .
It should be brought into the time domain and have
.
It should be brought into the time domain and have
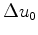 set to zero.
More simply, the mean can be removed in the Fourier domain.
set to zero.
More simply, the mean can be removed in the Fourier domain.
Causal least squares theory in a stationary world
says the signal output 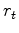 is white (Claerbout, 2009);
the autocorrelation of the signal output is a delta function.
Noncausal sparseness theory (other penalty functions) in a world of echoes (nonstationary gain)
says the
crosscorrelation of the signal output
with its gained softclip
is also a delta function
(equation (16), upon convergence).
is white (Claerbout, 2009);
the autocorrelation of the signal output is a delta function.
Noncausal sparseness theory (other penalty functions) in a world of echoes (nonstationary gain)
says the
crosscorrelation of the signal output
with its gained softclip
is also a delta function
(equation (16), upon convergence).
|
|
|
|
Decon in the log domain with variable gain |