|
|
|
|
Polarity preserving decon in ``N log N'' time |
Start with 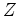 -transforms.
Given a time function
-transforms.
Given a time function
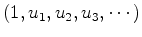 its
its 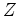 -transform is
-transform is
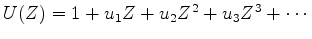 .
When you identify
.
When you identify
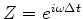 and
and
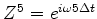 the
the 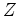 -transform is clearly a Fourier series.
An example of a causal function is
-transform is clearly a Fourier series.
An example of a causal function is 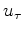 .
It is causal because
.
It is causal because 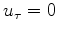 for
for 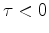 likewise,
likewise,
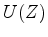 has no powers of
has no powers of 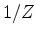 .
.
We may exponentiate 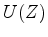 by a frequency domain method or a time domain method.
Easiest is the frequency domain method.
Write
by a frequency domain method or a time domain method.
Easiest is the frequency domain method.
Write
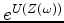 for all
for all 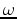 ,
then Fourier transform to time.
More interesting is the time domain method.
The polynomial U has no powers of
,
then Fourier transform to time.
More interesting is the time domain method.
The polynomial U has no powers of 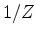 .
The power series for an exponential is
.
The power series for an exponential is
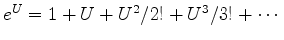 .
Inserting the polynomial for U into the power series for
.
Inserting the polynomial for U into the power series for 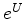 gives us a new polynomial (infinite series) that has no powers of
gives us a new polynomial (infinite series) that has no powers of 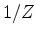 .
Furthermore, this new polynomial
always converges because of the powerful influence of the denominator factorials.
Thus we have shown that the ``exponential of a causal is a causal''.
.
Furthermore, this new polynomial
always converges because of the powerful influence of the denominator factorials.
Thus we have shown that the ``exponential of a causal is a causal''.
Let
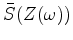 be an amplitude spectrum
be an amplitude spectrum
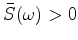 with logarithm
with logarithm
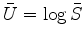 .
The exponential is the inverse of the logarithm
.
The exponential is the inverse of the logarithm
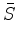 |
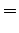 |
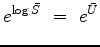 |
(1) |
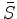 and
and 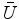 are real symmetric functions of
are real symmetric functions of 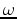 .
In the time domain,
.
In the time domain,
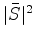 corresponds to an autocorrelation.
In the time domain,
corresponds to an autocorrelation.
In the time domain, 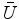 merely corresponds to a real symmetric function
merely corresponds to a real symmetric function
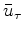 .
Adding some phase function
.
Adding some phase function
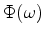 to
to 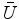 will shift the time function
will shift the time function 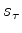 ,
likely shifting each frequency differently.
,
likely shifting each frequency differently.
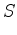 |
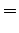 |
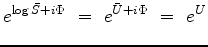 |
(2) |
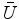 fixed keeps the spectrum
fixed keeps the spectrum 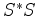 fixed.
Let
fixed.
Let 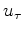 now correspond to the Fourier transform of
now correspond to the Fourier transform of
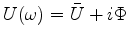 .
The time symmetric part of
.
The time symmetric part of 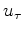 corresponds to
corresponds to
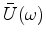 while the antisymmetric part of
while the antisymmetric part of 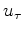 corresponds to the newly added phase
corresponds to the newly added phase
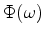 .
How shall we choose
.
How shall we choose
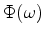 ?
Let us choose the antisymmetric part of
?
Let us choose the antisymmetric part of 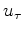 instead,
choose it to cancel the symmetric part of
instead,
choose it to cancel the symmetric part of 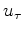 on the negative
on the negative 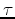 axis.
In other words, let us choose
axis.
In other words, let us choose 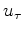 to be causal.
Recalling that ``exponentials of causals are causal''
we have thus created a causal
to be causal.
Recalling that ``exponentials of causals are causal''
we have thus created a causal 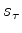 .
Hooray!
Hooray because
.
Hooray!
Hooray because 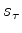 has the same spectrum
has the same spectrum 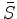 that we started with.
We started with a spectrum
that we started with.
We started with a spectrum 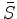 and constructed a causal wavelet
and constructed a causal wavelet 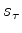 with that spectrum.
Good trick!
This is called ``spectral factorization.''
Causal decon is simply taking your data
with that spectrum.
Good trick!
This is called ``spectral factorization.''
Causal decon is simply taking your data 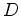 and dividing by a causal source waveform
and dividing by a causal source waveform 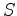 .
.
|
|
|
|
Polarity preserving decon in ``N log N'' time |