|
|
|
|
VTI migration velocity analysis using RTM |
First, for each image slice in the subsurface-offset domain 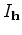 , we
compute a weighted image
, we
compute a weighted image
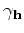 using equation 27. Then
we move on to equation 25. We can rearrange the independent and commutable
operators as follows:
using equation 27. Then
we move on to equation 25. We can rearrange the independent and commutable
operators as follows:
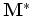 corresponds to differentiating
corresponds to differentiating 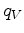 and
and 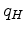 once reversely in time and setting
once reversely in time and setting 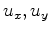 , and
, and 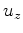 fields to zero. Notice that
the directions of propagation and differentiation in time of wavefield
fields to zero. Notice that
the directions of propagation and differentiation in time of wavefield 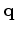 are the same. Therefore, we can compute the time derivative during the
same process as the propagation.
Then we shift the reverse-time derivative
are the same. Therefore, we can compute the time derivative during the
same process as the propagation.
Then we shift the reverse-time derivative 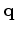 by
by 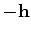 in
in 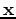 ,
and multiply it with the weighted image
,
and multiply it with the weighted image
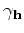 . This product
is shifted again by
. This product
is shifted again by 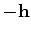 . Finally, we sum over the contributions
from all subsurface-offset image slices to get an effective source term
. Finally, we sum over the contributions
from all subsurface-offset image slices to get an effective source term
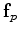 . Next, we solve equation 33 for
. Next, we solve equation 33 for
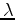 backward in time, using
backward in time, using 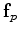 as the source.
as the source.
At the same time, in equation 28
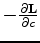 is a sparse matrix, with non-zero elements only for
is a sparse matrix, with non-zero elements only for 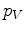 and
and 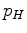 . We can
therefore write everything out explicitly:
. We can
therefore write everything out explicitly:
|
|
|
|
VTI migration velocity analysis using RTM |