 |
 |
 |
 | VTI migration velocity analysis using RTM |  |
![[pdf]](icons/pdf.png) |
Next: Lagrangian augmented functional method
Up: Migration Velocity Analysis Gradients
Previous: Migration Velocity Analysis Gradients
A perturbation, 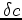 , of the velocity model
, of the velocity model 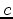 , induces a
perturbation
, induces a
perturbation
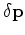 in the source wavefield vector
in the source wavefield vector 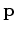 ,
a perturbation
,
a perturbation
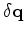 in the receiver wavefield vector
in the receiver wavefield vector 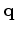 ,
a perturbation
,
a perturbation
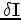 in the extended image cube
in the extended image cube 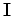 ,
and hence a perturbation
,
and hence a perturbation 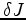 in the objective function
in the objective function 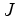 .
To the first order and using chain rule,
.
To the first order and using chain rule, 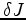 and
and 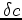 have
following relationship:
have
following relationship:
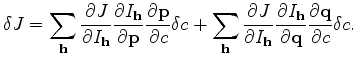 |
(16) |
Now we can define the gradient by the back-projection of a unit
perturbation in the objective function:
Let's analyze the first term in equation 17 in detail,
and the second term follows the same reasoning.
where
and
Plugging equation 19 and 20 into equation 18, we can
rewrite equation 18 explicitly as follows:
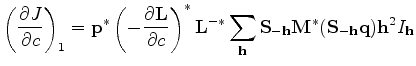 |
(21) |
Similarly, we can obtain the explicit form for the second term in
equation 17:
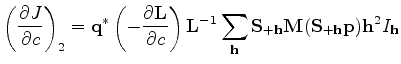 |
(22) |
Substituting equation 21 and equation 22
for the corresponding terms in equation 17,
we now have derived the explicit form for the DSO gradient.
 |
 |
 |
 | VTI migration velocity analysis using RTM |  |
![[pdf]](icons/pdf.png) |
Next: Lagrangian augmented functional method
Up: Migration Velocity Analysis Gradients
Previous: Migration Velocity Analysis Gradients
2012-05-10
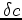 , of the velocity model
, of the velocity model 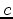 , induces a
perturbation
, induces a
perturbation
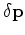 in the source wavefield vector
in the source wavefield vector 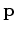 ,
a perturbation
,
a perturbation
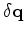 in the receiver wavefield vector
in the receiver wavefield vector 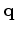 ,
a perturbation
,
a perturbation
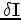 in the extended image cube
in the extended image cube 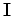 ,
and hence a perturbation
,
and hence a perturbation 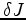 in the objective function
in the objective function 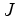 .
To the first order and using chain rule,
.
To the first order and using chain rule, 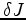 and
and 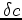 have
following relationship:
have
following relationship: