|
|
|
|
Tomographic full waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity analysis |
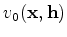 is the background component
and
is the background component
and
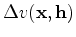 is the perturbation component,
i.e. the model update.
After this separation, the first-order Born approximation can
be used to define the gradient as follows:
is the perturbation component,
i.e. the model update.
After this separation, the first-order Born approximation can
be used to define the gradient as follows:
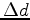 are the data residuals
and
are the data residuals
and 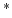 indicates the complex conjugate.
Unlike the usual linearization of the wave equation, the scattering term includes a Laplacian operator instead of the second derivative in time. The Laplacian operator does not add to the computational cost since it is already computed in the propagation of the background wavefield.
indicates the complex conjugate.
Unlike the usual linearization of the wave equation, the scattering term includes a Laplacian operator instead of the second derivative in time. The Laplacian operator does not add to the computational cost since it is already computed in the propagation of the background wavefield.
|
|
|
|
Tomographic full waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity analysis |