|
|
|
|
Tomographic full waveform inversion: Practical and computationally feasible approach |
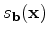 is the search direction of the background model and
is the search direction of the background model and
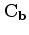 is a low-pass filter. Similarly, we can compute the update of the perturbation model as:
is a low-pass filter. Similarly, we can compute the update of the perturbation model as:
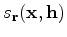 is the search direction of the perturbation model and
is the search direction of the perturbation model and
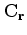 is a high-pass filter. In order to sum the two gradients properly, both of them need to have the same units as well as the same scale. This requires careful implementation of each operator at each linearization.
is a high-pass filter. In order to sum the two gradients properly, both of them need to have the same units as well as the same scale. This requires careful implementation of each operator at each linearization.
For the examples shown in this paper, we used a radial cut-off in the Fourier domain with a cosine squared taper. The wavelength cut-off is based on the dominant frequency in the data as well as the average velocity of the initial model. Also, the two filters were designed such that they always sum to one at all wavelength to maintain the energy of the gradients.
|
|
|
|
Tomographic full waveform inversion: Practical and computationally feasible approach |