|
|
|
|
Tomographic full waveform inversion: Practical and computationally feasible approach |
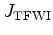 which can be written as:
which can be written as:
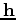 is the offset,
is the offset,
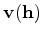 is the extended velocity model,
is the extended velocity model,
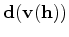 is the modeled data,
is the modeled data,
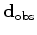 is the observed surface data,
is the observed surface data, 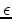 is a scalar weight of the regularization term and
is a scalar weight of the regularization term and 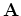 is a regularization operator. The modeled data
is a regularization operator. The modeled data
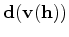 is computed as:
is computed as:
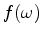 is the source function,
is the source function, 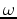 is frequency,
is frequency,
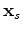 and
and
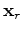 are the source and receiver coordinates, and
are the source and receiver coordinates, and 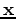 is the model coordinate. In the acoustic, constant-density case the Green's function
is the model coordinate. In the acoustic, constant-density case the Green's function
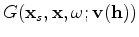 satisfies:
satisfies:
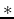 denotes a convolution operator over the subsurface offset axis (Symes, 2008; Biondi and Almomin, 2012).
The first simplification of the extended velocity model is to separate it into a background and a perturbation as follows:
denotes a convolution operator over the subsurface offset axis (Symes, 2008; Biondi and Almomin, 2012).
The first simplification of the extended velocity model is to separate it into a background and a perturbation as follows:
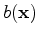 is the background component, which is a smooth version of the slowness squared and
is the background component, which is a smooth version of the slowness squared and
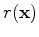 is the perturbation component. This separation assumes that
is the perturbation component. This separation assumes that
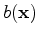 will contain the transmission effects and
will contain the transmission effects and
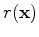 will contain the reflection effects. Depending on the error of the initial background velocity, the perturbation component can extend across several subsurface offsets so it is important to keep its offset axis. On the other hand, the background component is not expected to generate reflections that would be grossly time shifted with respect to the recorded data, and it thus safe to restrict it to zero offset. A physical interpretation is that the wave speed is not expected to vary much across different angles, at least in the isotropic case that we are analyzing. Therefore, the extent of background component across subsurface offsets can be reduced. If the velocity is expected to vary, the same reduction can be applied while keeping more than zero subsurface offset. In our derivation, we reduce the background to only the zero subsurface offset as follows
will contain the reflection effects. Depending on the error of the initial background velocity, the perturbation component can extend across several subsurface offsets so it is important to keep its offset axis. On the other hand, the background component is not expected to generate reflections that would be grossly time shifted with respect to the recorded data, and it thus safe to restrict it to zero offset. A physical interpretation is that the wave speed is not expected to vary much across different angles, at least in the isotropic case that we are analyzing. Therefore, the extent of background component across subsurface offsets can be reduced. If the velocity is expected to vary, the same reduction can be applied while keeping more than zero subsurface offset. In our derivation, we reduce the background to only the zero subsurface offset as follows
 is the Born modeling operator. We now define a new objective function for the efficient TFWI inversion as:
is the Born modeling operator. We now define a new objective function for the efficient TFWI inversion as:
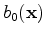 is the current background model and
is the current background model and
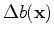 is the perturbation of the background. The Born approximation is used again to linearize the
is the perturbation of the background. The Born approximation is used again to linearize the 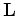 operator with respect to the background resulting in a data-space tomographic operator. The data perturbation with respect to the background perturbation is now defined as:
operator with respect to the background resulting in a data-space tomographic operator. The data perturbation with respect to the background perturbation is now defined as:
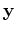 is the perturbation coordinates.
As we can see in the previous equation, the tomographic operator correlates a background and a scattered wavefield from both source and receiver sides. The scattered wavefields are computed by correlating a background wavefield with the reflectivity model
is the perturbation coordinates.
As we can see in the previous equation, the tomographic operator correlates a background and a scattered wavefield from both source and receiver sides. The scattered wavefields are computed by correlating a background wavefield with the reflectivity model 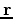 and then propagating again to all model locations.
The forward tomographic operator can be written in a compact notation as follows:
and then propagating again to all model locations.
The forward tomographic operator can be written in a compact notation as follows:
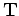 is the tomographic operator that relates changes in the background model to changes in the data. We can now compute the reflectivity gradient as follows:
is the tomographic operator that relates changes in the background model to changes in the data. We can now compute the reflectivity gradient as follows:
|
|
|
|
Tomographic full waveform inversion: Practical and computationally feasible approach |