Preconditioning a non-linear problem and its application to bidirectional deconvolution

GALI-PEF versus PEF preconditioning

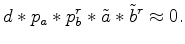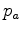In the previous subsections, we showed theoretically that prior knowledge from preconditioners $p_a$ and $p_b$ leads bidirectional deconvolution to the global minimum in the nonlinear problem. We have various choices of preconditioners to indicate different prior knowledge. Here we present two kinds of preconditioning, prediction-error filter(PEF) preconditioning and gapped anti-causal leaky integration followed by PEF (GALI-PEF) preconditioning.

The PEF, whose output is white, is widely used for deconvolution in standard industry practice. The expectation of whiteness in deconvolution encourages us to use PEF as our preconditioner. Thus we choose PEF as the preconditioner 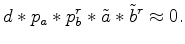$p_a$ and a spike as the preconditioner 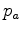$p_b$ in PEF preconditioning. Recall that a PEF is a causal filter with a causal inverse. Theoretically, this property adds confidence that deconvolution with a PEF might retrieve the correct phase spectrum as well as the correct amplitude spectrum. However, the wavelet we aim to estimate is not always causal -- can be mixed-phase. In most field data --such as band-limited marine seismic data or land response of an accelerometer --the wavelet is similar to a Ricker wavelet. It is dangerous to deal only with the causal part of the data by using PEF, because it may mislead the bidirectional deconvolution to an incorrect phase spectrum and into an unwelcome local minimum.

Therefore, utilizing the prior knowledge of the anti-causal part of the data becomes necessary. A finite representation of the Ricker wavelet is the negative of the second finite difference of some binomial coefficients. In Z-transform representation, this is

$$[(1-1/z)(1-z)][(1+1/z)^N(1+z)^N],$$ (9)

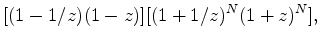where $N$ is the order of the binomial coefficient. In real cases, such as the marine data example, there is a time gap between the first ghost and first arrival; thus the numerical representation of the wavelet becomes

$$[(1-(\rho /z)^g)(1-(\rho z)^g)][(1+1/z)^N(1+z)^N],$$ (10)

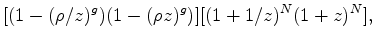where $g$ is an integer which indicates the length of the gap, and 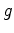$\rho$ is a real number which reduces the energy in a trace and deals with the situation where the gap is not an integer. With this numerical representation of the wavelet, we can divide the data by $[(1-(\rho /z)^g)]$ to estimate the anti-causal part of the wavelet. The inverse of $[(1-(\rho /z)^g)]$ is gapped anti-causal leaky integration, which is used as preconditioner $p_b$ . 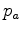After convolving the data with 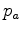$p_b$ , we apply a PEF to the convolution result and use this estimated PEF as preconditioner 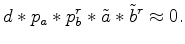$p_a$ . We hope this GALI-PEF preconditioning leads the bi-directional deconvolution to the correct phase spectrum and makes the result fall into the global minimum.

Preconditioning a non-linear problem and its application to bidirectional deconvolution