 |
 |
 |
 | Krylov space solver in Fortran 2009: Beta version |  |
![[pdf]](icons/pdf.png) |
Next: Example
Up: Operator-based object-oriented solvers
Previous: Combining operators
An iterative solver operates one a problem that can be described as simply
as equation 1. Translating a complicated problem into
this simple form is a more
complex problem. The problem is broken up into three steps: obtaining
an initial residual, finding the vector that best solves the constructed
inverse problem, and updating the model according to this vector. Each
one of these steps involve several different potential user inputs. For
simplicity, I am going to describe all potential inversion problems in
terms of a regularized inversion problem with two fitting goals
(each goal could be actually multiple fitting
goals combined using the functions described above).
The first step involves constructing the data space vectors, 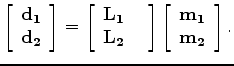 and
and 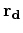 .
The user might begin by specifying some initial values for these two vectors. These values
then need to be updated according to the
data
.
The user might begin by specifying some initial values for these two vectors. These values
then need to be updated according to the
data 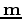 associated with the problem, a potential
initial model
associated with the problem, a potential
initial model 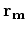 , the operators being used
, the operators being used
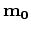 , and
weights applied to the residual
, and
weights applied to the residual
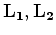 .
.
![$\displaystyle \left[ \begin{array}{c} \bf r_d \\ \bf r_m \\ \end{array} \right]...
...t[ \begin{array}{c} \bf L_1 \\ \bf L_2 \\ \end{array} \bf m_0 \right] \right ).$](img33.png) |
(7) |
Once the initial residual is calculated, we iterate to find
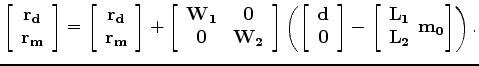 through,
through,
![$\displaystyle \left[ \begin{array}{c} \bf r_d \\ \bf r_m \\ \end{array} \right]...
...ray}{c} \bf W_1 \bf L_1 \\ \bf W_2 \bf L_2 \\ \end{array} \right] \bf S \bf x ,$](img35.png) |
(8) |
where 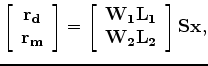 is a preconditioning operator.
Finally we need update our model,
is a preconditioning operator.
Finally we need update our model,
 |
(9) |
This procedure allows a single solver to be written for a myriad of
different inverse problems. It also demonstrates one of the biggest weaknesses
of Fortran 90. Fortran 90 does not support function pointers. As a result, SEP
has traditionally written different solvers for regularized and preconditioned
problems. Combination operators could only
be created by writing a function that specifically named
the two operators that were to be combined. As a result, creating
complex inversion problems quickly became cumbersome and prone
to errors.
 |
 |
 |
 | Krylov space solver in Fortran 2009: Beta version |  |
![[pdf]](icons/pdf.png) |
Next: Example
Up: Operator-based object-oriented solvers
Previous: Combining operators
2011-09-13
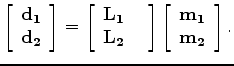 and
and ![]() .
The user might begin by specifying some initial values for these two vectors. These values
then need to be updated according to the
data
.
The user might begin by specifying some initial values for these two vectors. These values
then need to be updated according to the
data ![]() associated with the problem, a potential
initial model
associated with the problem, a potential
initial model ![]() , the operators being used
, the operators being used
![]() , and
weights applied to the residual
, and
weights applied to the residual
![]() .
.
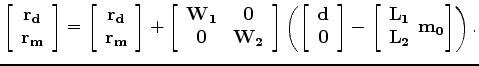 through,
through,
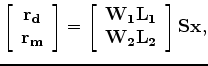 is a preconditioning operator.
Finally we need update our model,
is a preconditioning operator.
Finally we need update our model,