 |
 |
 |
 | Krylov space solver in Fortran 2009: Beta version |  |
![[pdf]](icons/pdf.png) |
Next: Combining operators
Up: Operator-based object-oriented solvers
Previous: Vector class
The base operator class contains the ability to perform
a mapping from the vector-space of the operators domain,
to the vector space of operator's range (the
forward of the operator), and vice versa (applying the adjoint).
It is beneficial
for an operator to store a description of these two spaces
(the reason for the clone-space function described above).
This performs two functions. First, the operator can
perform a sanity check to make sure that the spaces of
model and data
passed into the forward or adjoint function call match
the space of initialized domain and range. The second
reason is that inversion problems are often more
complicated then the generic problem described by
equation 1. For example, if 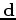 is actually the cascade of two operator
is actually the cascade of two operator 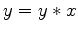 and
and  ,
,
 |
(2) |
we need the ability to check that the domain of is 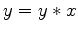 is equivalent to the range of
is equivalent to the range of  and we need to
create a vector of that size to hold the intermediate
result of applying
and we need to
create a vector of that size to hold the intermediate
result of applying  in the forward case (and
in the forward case (and 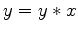 in
the case of the adjoint).
in
the case of the adjoint).
A Fortran 2008 type must be declared in a module. An example
of an operator declaration is seen below. In this case I am creating
a causal integration operator.
module causal_mod
use operator_mod !Description of the generic operator class
use vec_nd_mod !The specific vector class used in this module
implicit none
type,extends(operator) ::causint_op !Causint operator declaration
contains
procedure,pass :: op=>causint_it !Pointer to the generic forward/adj
final:: causint_close !clean function (not necessary in this case)
end type
When leaving a functional unit that has declared a type or when deallocating
a type the final function is called. In this case we haven't allocated
any memory but for completeness, and for debugging, it is often useful to include
it.
subroutine causint_close(myop)
type(causint_op) :: myop
end subroutine
We need a subroutine that sets up a causal integration operator. The only
information we need is the size of the vector space in which we are going to be
performing causal integration on.
subroutine create_causint_op(myop,v)
class(vector) :: v !vector space we are operating on
class(causint_op) :: myop !operator we are setting up
logical :: bm=.false. !default to having the wrong type of vector
myop%lab=l
select type(v) !check the type of vector
class is (real_1d) !make sure it is a 1-D real vector
bm=.true. !we have the right type of vector
end select
if(.not. bm) call seperr("model and vector must be real_1d")
call myop%set_domain_range(v,v) !store the domain and range
end subroutine
The only thing left is the actual operator. I am going to break it
into to parts. The first part is the initialization and the overhead associated
with Fortran 2008.
subroutine causint_it(myop,adj,add,mod,dat)
class(causint_op) :: myop !causal integration object
logical, intent(in) :: adj,add
class(vector) :: mod,dat !vector spaces
real,dimension(:), pointer :: xx,yy
real,dimension(:,:),pointer :: ar
integer :: i,j,nm,nd
real :: t
!Check to make sure the model and data vector
!spaces match those stored in the operator declaration
if(.not. mod%check_same(myop%domain))&
call seperr("domains don't match")
if(.not. dat%check_same(myop%range)) &
call seperr("ranges don't match")
call adj_null(adj,add,mod,dat)
!Create a pointer to the model values
select type(mod)
class is (real_1d)
xx=>mod%vals
nm=size(mod%vals)
end select
!Create a pointer to the data values
select type(dat)
class is (real_1d)
yy=>dat%vals
nd=size(dat%vals)
end select
The second part is standard Fortran77/90/2003/2008.
t=0
if(adj) then
do i= nd, 1, -1
t = t + yy(i)
xx(i) = xx(i) + t
end do
else
do i= 1, nd
t = t + xx(i)
yy(i) = yy(i) + t
end do
end if
end subroutine
end module
 |
 |
 |
 | Krylov space solver in Fortran 2009: Beta version |  |
![[pdf]](icons/pdf.png) |
Next: Combining operators
Up: Operator-based object-oriented solvers
Previous: Vector class
2011-09-13