 |
 |
 |
 | Moveout-based wave-equation migration velocity analysis |  |
![[pdf]](icons/pdf.png) |
Next: Appendix-B
Up: Appendix-A
Previous: Appendix-A
This section illustrates how to calculate the sensitivity kernel of the image shift parameter
 :
:
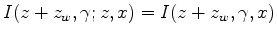 .
Since
.
Since 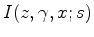 maximizes the auxillary objective function,
maximizes the auxillary objective function,
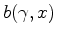 for each z,x for each z,x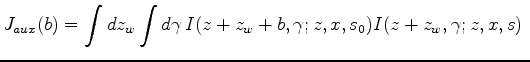 |
(7) |
we have
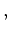 |
(8) |
To find the relation between 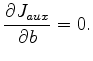 and
and 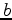 , we differentiate equation (8) with respect to
, we differentiate equation (8) with respect to 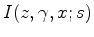 and
and 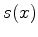 , which yields
, which yields
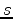 |
(9) |
in which we can find
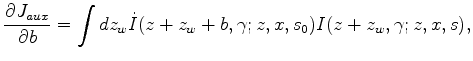 indicate the first and second derivatives in
indicate the first and second derivatives in 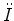 (depth). Let
(depth). Let
Then substituting the above two equations into eq. (9) leads to
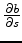 |
(10) |
which is eq. (2).
 |
 |
 |
 | Moveout-based wave-equation migration velocity analysis |  |
![[pdf]](icons/pdf.png) |
Next: Appendix-B
Up: Appendix-A
Previous: Appendix-A
2011-05-24
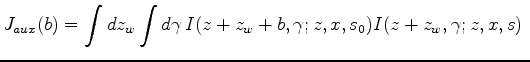
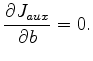 and
and ![]() , we differentiate equation (8) with respect to
, we differentiate equation (8) with respect to ![]() and
and ![]() , which yields
, which yields
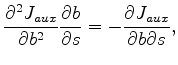
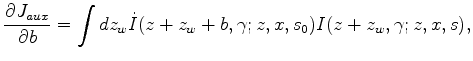 indicate the first and second derivatives in
indicate the first and second derivatives in